Reverse mode automatic differentiation is kind of like a lens. Here is the type for a non-fancy lens

type Lens s t a b = s -> (a, b -> t)

When you compose two lenses, you compose the getters (s -> a) and you compose the partially applied setter (b -> t) in the reverse direction.

We can define a type for a reverse mode differentiable function

type AD x dx y dy = x -> (y, dy -> dx)

When you compose two differentiable functions you compose the functions and you flip compose the Jacobian transpose (dy -> dx). It is this flip composition which gives reverse mode it’s name. The dependence of the Jacobian on the base point x corresponds to the dependence of the setter on the original object

The implementation of composition for Lens and AD are identical.

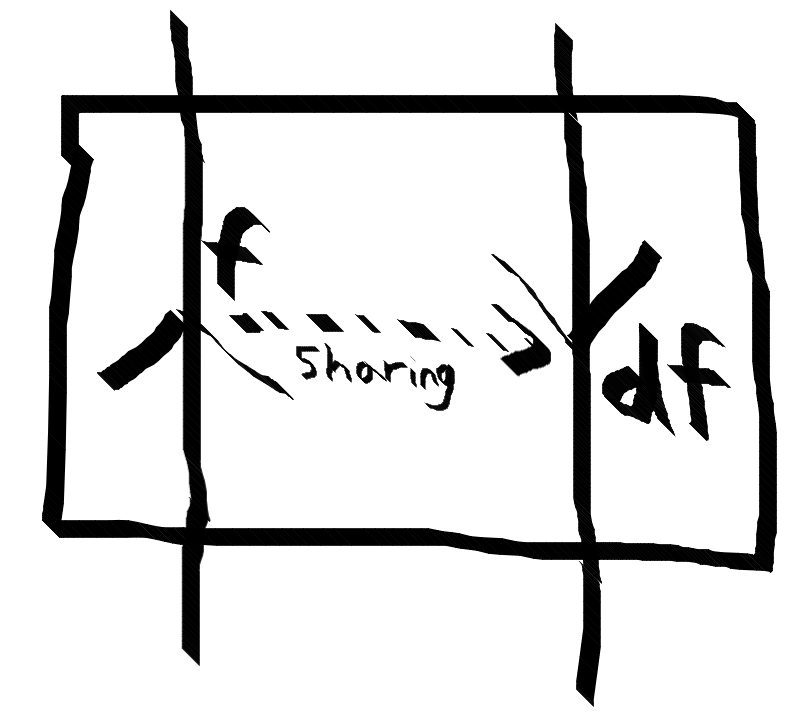
Both of these things are described by the same box diagram (cribbed from the profunctor optics paper www.cs.ox.ac.uk/people/jeremy.gibbons/publications/poptics.pdf ).

This is a very simple way of implementing a reserve mode automatic differentiation using only non exotic features of a functional programming language. Since it is so bare bones and functional, is this a good way to achieve the vision gorgeous post by Christoper Olah?  http://colah.github.io/posts/2015-09-NN-Types-FP/  I do not know.

Now, to be clear, these ARE NOT lenses. Please, I don’t want to cloud the water, do not call these lenses. They’re pseudolenses or something. A very important part of what makes a lens a lens is that it obeys the lens laws, in which the getter and setter behave as one would expect. Our “setter” is a functional representation of the Jacobian transpose and our getter is the function itself. These do not obey lens laws in general.

Chain Rule and Jacobians

What is reverse mode differentiation? One’s thinking is muddled by defaulting to the Calc I perspective of one dimensional functions. Thinking is also muddled by  the general conception that the gradient is a vector. This is slightly sloppy talk and can lead to confusion. It definitely has confused me.

The right setting for intuition is $ R^n \rightarrow R^m$ functions

If one looks at a multidimensional to multidimensional function like this, you can form a matrix of partial derivatives known as the Jacobian. In the scalar to scalar case this is a $ 1\times 1$ matrix, which we can think of as just a number. In the multi to scalar case this is a $ 1\times n$ matrix which we somewhat fuzzily can think of as a vector.

The chain rule is a beautiful thing. It is what makes differentiation so elegant and tractable.

For many-to-many functions, if you compose them you matrix multiply their Jacobians.

Just to throw in some category theory spice (who can resist), the chain rule is a functor between the category of differentiable functions and the category of vector spaces where composition is given by Jacobian multiplication. This is probably wholly unhelpful.

The chain rule says that the derivative operator is a functor.

— Functor Fact (@FunctorFact) September 13, 2018

The cost of multiplication for an $ a \times b$ matrix A and an $ b \times c$ matrix B is $ O(abc) $. If we have 3 matrices ABC, we can associate to the left or right. (AB)C vs A(BC) choosing which product to form first. These two associations have different cost, abc * acd for left association or abd * bcd for right association. We want to use the smallest dimension over and over. For functions that are ultimately many to scalar functions, that means we want to multiply starting at the right.

For a clearer explanation of the importance of the association, maybe this will help https://en.wikipedia.org/wiki/Matrix_chain_multiplication

Functional representations of matrices

A Matrix data type typically gives you full inspection of the elements. If you partially apply the matrix vector product function (!* :: Matrix -> Vector -> Vector) to a matrix m, you get a vector to vector function (!* m) :: Vector -> Vector. In the sense that a matrix is data representing a linear map, this type looks gorgeous. It is so evocative of purpose.

If all you want to do is multiply matrices or perform matrix vector products this is not a bad way to go. A function in Haskell is a thing that exposes only a single interface, the ability to be applied. Very often, the loss of Gaussian elimination or eigenvalue decompositions is quite painfully felt. For simple automatic differentiation, it isn’t so bad though.

You can inefficiently reconstitute a matrix from it’s functional form by applying it to a basis of vectors.

One weakness of the functional form is that the type does not constrain the function to actually act linearly on the vectors.

One big advantage of the functional form is that you can intermix different matrix types (sparse, low-rank, dense) with no friction, just so long as they all have some way of being applied to the same kind of vector. You can also use functions like (id :: a -> a) as the identity matrix, which are not built from any underlying matrix type at all.

To match the lens, we need to represent the Jacobian transpose as the function (dy -> dx) mapping differentials in the output space to differentials in the input space.

The Lens Trick

A lens is the combination of a getter (a function that grabs a piece out of a larger object) and a setter (a function that takes the object and a new piece and returns the object with that piece replaced).

The common form of lens used in Haskell doesn’t look like the above. It looks like this.

type Lens s t a b = forall f. Functor f => (a -> f b) -> (s -> f t)

This form has exactly the same content as the previous form (A non obvious fact. See the Profunctor Optics paper above. Magic neato polymorphism stuff), with the added functionality of being able to compose using the regular Haskell (.) operator.

I think a good case can be made to NOT use the lens trick (do as I say, not as I do). It obfuscates sharing and obfuscates your code to the compiler (I assume the compiler optimizations have less understanding of polymorphic functor types than it does of tuples and functions), meaning the compiler has less opportunity to help you out. But it is also pretty cool. So… I dunno. Edit:

/u/mstksg points out that compilers actually LOVE the van Laarhoven representation (the lens trick) because when f is finally specialized it is a newtype wrappers which have no runtime cost. Then the compiler can just chew the thing apart.

https://www.reddit.com/r/haskell/comments/9oc9dq/reverse_mode_differentiation_is_kind_of_like_a/

One thing that is extra scary about the fancy form is that it makes it less clear how much data is likely to be shared between the forward and backward pass. Another alternative to the lens that shows this is the following.

type AD x dx y dy = (x -> y, x -> dy -> dx)

This form is again the same in end result. However it cannot share computation and therefore isn’t the same performance wise. One nontrivial function that took me some head scratching is how to convert from the fancy lens directly to the regular lens without destroying sharing. I think this does it

unfancy :: Lens' a b -> (a -> (b, b -> a))
unfancy l = getCompose . l (\b -> Compose (b, id))

Some code

I have some small exploration of the concept in this git https://github.com/philzook58/ad-lens

Again, really check out Conal Elliott’s AD paper and enjoy the many, many apostrophes to follow.

Some basic definitions and transformations between fancy and non fancy lenses. Extracting the gradient is similar to the set function. Gradient assumes a many to one function and it applies it to 1.

import Data.Functor.Identity
import Data.Functor.Const
import Data.Functor.Compose

type Lens' a b = forall f. Functor f => (b -> f b) -> a -> f a

lens'' :: (a -> (b, b -> a)) -> Lens' a b
lens'' h g x = fmap j fb where
    (b, j) = h x
    fb = g b

over :: Lens' a b -> ((b -> b) -> a -> a)
over l f = runIdentity . l (Identity . f)

set :: Lens' a b -> a -> b -> a
set l = flip (\x -> (over l (const x)))

view :: Lens' a b -> a -> b
view l = getConst . l Const

unlens'' :: Lens' a b -> (a -> (b, b -> a))
unlens'' l = getCompose . l (\b -> Compose (b, id))

constlens :: Lens' (a,b) c -> b -> Lens' a c
constlens l b = lens'' $ \a -> let (c, df) = f (a,b) in
                                (c, fst . df) where 
                                            f = unlens'' l


grad :: Num b => Lens' a b -> a -> a
grad l = (flip (set l)) 1

Basic 1D functions and arrow/categorical combinators

-- add and dup are dual!

add' :: Num a => Lens' (a,a) a 
add' = lens'' $ \(x,y) -> (x + y, \ds -> (ds, ds))

dup' :: Num a => Lens' a (a,a)
dup' = lens'' $ \x -> ((x,x), \(dx,dy) -> dx + dy)

sub' :: Num a => Lens' (a,a) a 
sub' = lens'' $ \(x,y) -> (x - y, \ds -> (ds, -ds))

mul' :: Num a => Lens' (a,a) a 
mul' = lens'' $ \(x,y) -> (x * y, \dz -> (dz * y, x * dz))

recip' :: Fractional a => Lens' a a 
recip' = lens'' $ \x-> (recip x, \ds -> - ds / (x * x))

div' :: Fractional a => Lens' (a,a) a 
div' = lens'' $ (\(x,y) -> (x / y, \d -> (d/y,-x*d/(y * y))))

sin' :: Floating a => Lens' a a
sin' = lens'' $ \x -> (sin x, \dx -> dx * (cos x))

cos' :: Floating a => Lens' a a
cos' = lens'' $ \x -> (cos x, \dx -> -dx * (sin x))

pow' :: Num a => Integer -> Lens' a a
pow' n = lens'' $ \x -> (x ^ n, \dx -> (fromInteger n) * dx * x ^ (n-1)) 

--cmul :: Num a => a -> Lens' a a
--cmul c = lens (* c) (\x -> \dx -> c * dx)

exp' :: Floating a => Lens' a a
exp' = lens'' $ \x -> let ex = exp x in
                        (ex, \dx -> dx * ex)

fst' :: Num b => Lens' (a,b) a
fst' = lens'' (\(a,b) -> (a, \ds -> (ds, 0)))

snd' :: Num a => Lens' (a,b) b
snd' = lens'' (\(a,b) -> (b, \ds -> (0, ds)))

swap' :: Lens' (a,b) (b,a)
swap' = lens'' (\(a,b) -> ((b,a), \(db,da) -> (da, db)))

assoc' :: Lens' ((a,b),c) (a,(b,c))
assoc' = lens'' $ \((a,b),c) -> ((a,(b,c)), \(da,(db,dc)) -> ((da,db),dc))

par' :: Lens' a b -> Lens' c d -> Lens' (a,c) (b,d)
par' l1 l2 = lens'' f3 where
    f1 = unlens'' l1
    f2 = unlens'' l2
    f3 (a,c) = ((b,d), df1 *** df2) where
        (b,df1) = f1 a
        (d,df2) = f2 c

fan' :: Num a => Lens' a b -> Lens' a c -> Lens' a (b,c)
fan' l1 l2 = lens'' f3 where
    f1 = unlens'' l1
    f2 = unlens'' l2
    f3 a = ((b,c), \(db,dc) -> df1 db + df2 dc) where
        (b,df1) = f1 a
        (c,df2) = f2 a

first' :: Lens' a b -> Lens' (a, c) (b, c)
first' l = par' l id

second' :: Lens' a b -> Lens' (c, a) (c, b)
second' l = par' id l

relu' :: (Ord a, Num a) => Lens' a a
relu' = lens'' $ \x -> (frelu x, brelu x) where
        frelu x | x > 0 = x
                | otherwise = 0
        brelu x dy | x > 0 = dy
                    | otherwise = 0

Some List based stuff.

import Data.List (sort)
import Control.Applicative (ZipList (..))

-- replicate and sum are dual!

sum' :: Num a => Lens' [a] a
sum' = lens'' $ \xs -> (sum xs, \dy -> replicate (length xs) dy)

replicate' :: Num a => Int -> Lens' a [a]
replicate' n = lens'' $ \x -> (replicate n x, sum)

repeat' :: Num a => Lens' a [a]
repeat' = lens'' $ \x -> (repeat x, sum)

map' :: Lens' a b -> Lens' [a] [b]
map' l = lens'' $ \xs -> let (bs, fs) = unzip . map (unlens'' l) $ xs in 
                        (bs, getZipList . ((ZipList fs) <*>) . ZipList)

zip' :: Lens' ([a], [b]) [(a,b)]
zip' = lens'' $ \(as,bs) -> (zip as bs, unzip)

unzip' :: Lens' [(a,b)] ([a], [b])
unzip' = lens'' $ \xs -> (unzip xs, uncurry zip)

maximum' :: (Num a, Ord a) => Lens' [a] a
maximum' = lens'' $ \(x:xs) -> let (best, bestind, lenxs) = argmaxixum x 0 1 xs in
                                (best, \dy -> onehot bestind lenxs dy) where
    argmaxixum best bestind len [] = (best, bestind, len) 
    argmaxixum best bestind curind (x:xs) = if x > best then argmaxixum x curind (curind + 1) xs else argmaxixum best bestind (curind + 1) xs  
    onehot n m x | m == 0 = []
                    | n == m = x : (onehot n (m-1) x) 
                    | otherwise = 0 : (onehot n (m-1) x)

sort' :: Ord a => Lens' [a] [a]
sort' = lens'' $ \xs -> let (sxs, indices) = unzip . sort $ zip xs [0 ..] in
                        (sxs, desort indices) where
                            desort indices = snd . unzip . sort . zip indices

And some functionality from HMatrix

import Numeric.LinearAlgebra
import Numeric.LinearAlgebra.Devel (zipVectorWith)
import Numeric.ADLens.Lens
-- import Data.Vector as V

dot' :: (Container Vector t, Numeric t) => Lens' (Vector t, Vector t) t
dot' = lens'' $ \(v1,v2) -> (v1 <.> v2, \ds -> (scale ds v2, scale ds v1))

mdot' :: (Product t, Numeric t) => Lens' (Matrix t, Vector t) (Vector t)
mdot' = lens'' $ \(a,v) -> (a #> v, \dv -> (outer dv v, dv <# a))

add' :: Additive c => Lens' (c, c) c
add' = lens'' $ \(v1,v2) -> (add v1 v2, \dv -> (dv, dv))

-- I need konst I think?
sumElements' :: (Container Vector t, Numeric t) => Lens' (Vector t) t
sumElements' = lens'' $ \v -> (sumElements v, \ds -> scalar ds)

reshape' :: Container Vector t => Int -> Lens' (Vector t) (Matrix t)
reshape' n = lens'' $ \v -> (reshape n v,  \dm -> flatten dm)

-- conjugate transpose not trace
tr'' ::  (Transposable m mt, Transposable mt m) => Lens' m mt
tr'' = lens'' $ \x -> (tr x, \dt -> tr dt)


flatten' :: (Num t, Container Vector t) => Lens' (Matrix t) (Vector t)
flatten' = lens'' $ \m -> let s = fst $ size m in  
                            (flatten m,  \dm -> reshape s dm)


norm_2' :: (Container c R, Normed (c R), Linear R c) => Lens' (c R) R
norm_2' = lens'' $ \v -> let nv = norm_2 v in (nv, \dnv -> scale (2 * dnv / nv) v )



cmap' :: (Element b, Container Vector e) => (Lens' e b) -> Lens' (Vector e) (Vector b)
cmap' l = lens'' $ \c -> (cmap f c, \dc -> zipVectorWith f' c dc) where
        f = view l
        f' = set l
    
{-
maxElement' :: Container c e => Lens' (c e) e
maxElement' = lens'' $ \v -> let i = maxIndex v in (v ! i, dv -> scalar 0)
-}

det' :: Field t => Lens' (Matrix t) t
det' = lens'' $ \m -> let (minv, (lndet, phase)) = invlndet m in
                    let detm = phase * exp detm in
                    (detm, \ds -> (scale (ds * detm) minv))

diag' :: (Num a, Element a) => Lens' (Vector a) (Matrix a)
diag' = lens'' $ \v -> (diag v, takeDiag)

takeDiag' :: (Num a, Element a) => Lens' (Matrix a) (Vector a) 
takeDiag' = lens'' $ \m -> (takeDiag m, diag)

In practice, I don’t think this is a very ergonomic approach without something like Conal Elliott’s Compiling to Categories plugin. You have to program in a point-free arrow style (inspired very directly by Conal’s above AD paper) which is pretty nasty IMO. The neural network code here is inscrutable. It is only a three layer neural network.

    import Numeric.ADLens.Lens
    import Numeric.ADLens.Basic
    import Numeric.ADLens.List
    import Numeric.ADLens.HMatrix
    
    
    import Numeric.LinearAlgebra
    
    type L1 = Matrix Double
    type L2 = Matrix Double
    type L3 = Matrix Double
    
    
    
    type Input = Vector Double
    type Output = Vector Double
    type Weights = (L1,(L2,(L3,())))
    
    class TupleSum a where
    	tupsum :: a -> a -> a
    instance TupleSum () where
    	tupsum _ _ = ()
    instance (Num a, TupleSum b) => TupleSum (a,b) where
    	tupsum (a,x) (b,y) = (a + b, tupsum x y)
    
    -- A dense relu neural network example
    swaplayer :: Lens' ((Matrix t, b), Vector t) (b, (Matrix t, Vector t))
    swaplayer = first' swap' . assoc' 
    
    mmultlayer :: Numeric t => Lens' (b, (Matrix t, Vector t)) (b, Vector t)
    mmultlayer = second' mdot'
    
    relulayer :: Lens' (b, Vector Double) (b, Vector Double)
    relulayer = second' $ cmap' relu'
    
    uselayer :: Lens' ((Matrix Double, b), Vector Double) (b, Vector Double)
    uselayer = swaplayer . mmultlayer . relulayer
    
    runNetwork :: Lens' (Weights, Input) ((), Output)
    runNetwork =  uselayer . uselayer . uselayer
    
    main :: IO ()
    main = do
       putStrLn "Starting Tests"
       print $ grad (pow' 2) 1
       print $ grad (pow' 4) 1
       print $ grad (map' (pow' 2) . sum') $ [1 .. 5]
       print $ grad (map' (pow' 4) . sum') $ [1 .. 5]
       print $ map (\x -> 4 * x ^ 3 )  [1 .. 5]
       l1 <- randn 3 4
       l2 <- randn 2 3
       l3 <- randn 1 2
       let weights = (l1,(l2,(l3,())))
       print $ view runNetwork (weights, vector [1,2,3,4])
       putStrLn "The neural network gradients"
       print $ set runNetwork (weights, vector [1,2,3,4]) ((), vector [1])

For those looking for more on automatic differentiation in Haskell: