A very powerful methodology for modelling programs in a way amenable to verification is that of constrained horn clauses (CHC).

I have more notes on CHC here. I have put the code of this post here https://github.com/philzook58/nand2coq/tree/master/python

One way of looking at this encoding is how you model stateful calculations in prolog. Many questions of verification correspond to a reachability questions, which prolog can do via branching search for bad states. To sketch it out:

reachable(State) :- bad(State).
reachable(State) :- transition(State, State'), reachable(State').
?- init(State), reachable(State).

Where bad and transition are defined somewhere else in an application specific way.

When looked at logically, these are $\forall$ quantified statements.

$ \forall state, bad(state) \implies reachable(state) $ $ \forall state state’, transition(state, state’) \land reachable(state’) \implies reachable(state)$

A counter intuitive thing to me is that the query can be encoded as $ \forall state, init(state) \land reachable(state) \implies \bot $

And then the backwards chaining can be considered trying to find a refutation proof of false.

An important conceptual step between programming languages and state machines is to remember that the Program Counter exists. It is part of the state.

The Z3 SMT solver ships with a constrained horn clause solver, Spacer. I learned a lot from looking at the Dahgstuhl notes. There is also an alternative input syntax (“fixedpoint”) although here I do not use it. There are other solvers for horn clause style things in z3 including datalog and a bounded model checking mode.

The is something very confusing compared with the prolog model given above. Spacer returns a representation of the predicates when the prolog search would fail, and returns UNSAT and no model when the prolog counterexample search would succeed. So it’s sort of a different thing. Getting back a representation of the entire predicate is much more powerful. Also interesting, the prolog model corresponds to “backwards” invariant checking in the notes above.

This CHC methodology becomes particularly useful when you’re dealing with low level code, which is unstructured (in the sense of structured programming).

There is in some sense a hiearchy of partial evaluations you can do to the verficiation problem depending on how much you can analyze ahead of time. Since for example on the nand2tetris cpu, the program is stored in rom and is unchanging, we can remove the rom from the state and expand out the important lines of the program. If we statically know certain control flow possibility or possible values, we can profitably do other “compile time” transformations on our logical formulae.

The Nand2tetris course describes a very simple cpu. A fun thing to try is take the specification and interpret it into constrained horn clauses, and query Z3. This is a very simple way to build a verifier.

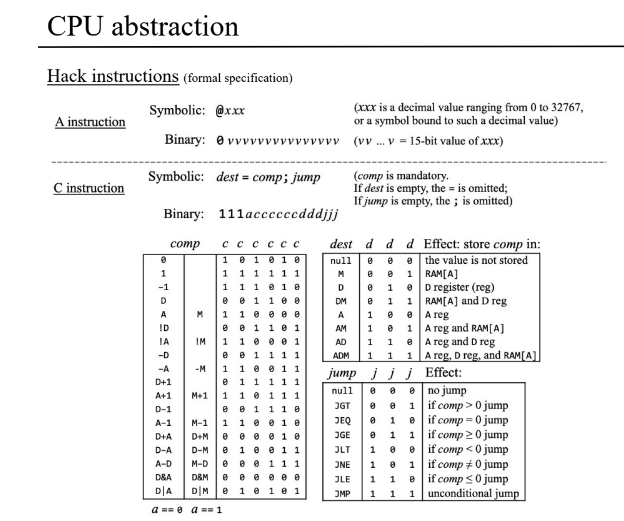
To do so, I made a small embedded DSL for writing nand2tetris programs and a translator from an instruction to a Z3 horn clause.

You can then ask it to check that two simple example programs do what their high level spec says. If it comes back SAT, that means Z3 discovered a sufficiently accurate descrption of the Insn predicate that describes the possible reachable states. An answer of UNSAT means that the Insn predicate does not exist, and in fact the Z3 proof of this fact contains in some sense a counterexample trace.

Once you define your data types, everything often becomes more clear. The Nand2Tetris cpu is very cleverly designed. By greatly limitting the number of registers of the machine, the notion of computation is fairly easily directly enumerable instead of require a seperation into operation and operands. This is weird and inelegant in one sense, but simplifies some other things quite a lot.

from dataclasses import dataclass
from enum import Enum       
from typing import List, Union

Comp = Enum('Comp', '''ZERO ONE NEGONE D A M NOTD NOTA NOTM NEGD NEGA NEGM INCD INCA INCM DECD DECA DECM 
                         ADD_DA ADD_DM SUB_DA SUB_DM SUB_AD SUB_MD AND_DA AND_DM OR_DA OR_DM''') 
Dest = Enum('Dest', 'NULL M D MD A AM AD AMD') 
Jump = Enum('Jump', 'NULL JGT JEQ JGE JLT JNE JLE JMP') 

@dataclass
class AInsn:
    lit: int

@dataclass
class CInsn:
    dest: Dest
    comp: Comp
    jump: Jump

@dataclass
class HackState:
    rA: int
    rD: int
    pc: int
    mem: List[int]

The following encodes the semantics of the cpu into a transition relation relating state variables and state variables at the next time step.

def jump_table(comp):
    return { 
    Jump.NULL: False,
    Jump.JGT: comp > 0,
    Jump.JEQ: comp == 0,
    Jump.JGE: comp >= 0,
    Jump.JLT: comp < 0,
    Jump.JNE: comp != 0,
    Jump.JLE: comp <= 0,
    Jump.JMP: True
    }

def comp_table(s):
    A = s.rA
    D = s.rD
    pc = s.pc
    M = s.mem(A)
    return {
        Comp.ZERO:  0,
        Comp.ONE: 1,
        Comp.NEGONE: -1,
        Comp.D: D,
        Comp.A: A,
        Comp.M: M,
        Comp.NOTD: ~D,
        Comp.NOTA: ~A,
        Comp.NOTM: ~M,
        Comp.NEGD: -D,
        Comp.NEGA: -A,
        Comp.NEGM: -M,
        Comp.INCD: D + 1,
        Comp.INCA: A + 1,
        Comp.INCM: M + 1,
        Comp.DECD: D - 1,
        Comp.DECA: A - 1,
        Comp.DECM: M - 1,
        Comp.ADD_DA: D + A,
        Comp.ADD_DM: D + M,
        Comp.SUB_DA: D - A,
        Comp.SUB_DM: D - M,
        Comp.SUB_AD: A - D,
        Comp.SUB_MD: M - D,
        Comp.AND_DA: D & A,
        Comp.AND_DM: D & M,
        Comp.OR_DA: D | A,
        Comp.OR_DM: D | M
    }

from z3 import *
# Defining a bunch of variables
BV16 = BitVecSort(16)
ramsize = 2
AddrSort = BitVecSort(ramsize)
A, D, PC, A1, D1, PC1 = BitVecs("A D PC A1 D1 PC1", BV16)

MEM = Array("RAM", AddrSort, BV16)
MEM1 = Array("RAM1", AddrSort, BV16)
RAM = lambda addr: MEM[Extract(ramsize-1,0,addr)]
RAM1 = lambda addr: MEM1[Extract(ramsize-1,0,addr)]


M = RAM(A)
M1 = RAM1(A1)

st = HackState(A,D,PC,RAM)
z3_comp_table = comp_table(st)

Insn = Function("Insn", BV16, BV16, BV16, ArraySort(AddrSort, BV16), BoolSort())

def z3_insn(insn):
    ''' Returns the transition relation corresponding to the given instruction'''
    if type(insn) == AInsn:
        return And([A1 == BitVecVal(insn.lit, 16), 
                    PC1 == PC + 1, 
                    D == D1, 
                    MEM == MEM1])
    elif type(insn) == CInsn:
        Trans = []

        comp1 = z3_comp_table[insn.comp]
        if insn.dest in [Dest.A, Dest.AD, Dest.AD, Dest.AMD]:
            Trans += [A1 == comp1]
        else:
            Trans += [A1 == A]

        if insn.dest == Dest.D or insn.dest == Dest.MD or insn.dest == Dest.AD or insn.dest == Dest.AMD:
            Trans += [D1 == comp1]
        else:
            Trans += [D1 == D]

        if insn.dest == Dest.M or insn.dest == Dest.MD or insn.dest == Dest.AM or insn.dest == Dest.AMD:
            Trans += [MEM1 == Store(MEM, Extract(ramsize-1,0,A), comp1)]
        else:
            Trans += [MEM1 == MEM]
        
        cond = jump_table(comp1)[insn.jump]
        Trans += [If(cond, PC1 == A, PC1 == PC + 1)]
        
        return And(Trans)

Finally the actual horn clause encoding (btw there are other ways of encoding this).

def horn(prog):
    clauses = []
    Init = PC == 0
    # Program starts at pc = 0, arbitrary data in registers and ram
    # This corresponds to the prolog "query" ?- line.
    clauses += [ForAll([A,A1,D,D1,PC,PC1,MEM,MEM1], Implies(And(Insn(A,D,PC,MEM),Init), False))]
    
    for pc, insn in enumerate(prog):
        # Build transition relation of instruction
        Trans = And(z3_insn(insn), PC == pc)
        clauses += [ForAll([A,A1,D,D1,PC,PC1,MEM,MEM1], 
                    Implies(And(Trans, Insn(A1,D1,PC1,MEM1)),
                            Insn(A,D,PC,MEM)))]
    return clauses

def assert_(prop):
    return ForAll([A, D, PC, MEM], Implies(Not(prop), Insn(A,D,PC,MEM) ))

I made a nicer-ish embedded dsl to side step parsing, which is part of the nand2tetris homework. This may have been a horrible idea.

def At(x):
    return AInsn(x)
def C(dest, comp, *jmp):
    if len(jmp) == 0:
        jmp = Jump.NULL
    else:
        assert len(jmp) == 1
        jmp = jmp[0]
    if comp == 0:
        comp = Comp.ZERO
    elif comp == 1:
        comp = Comp.ONE
    elif comp == -1:
        comp = Comp.NEGONE
    elif comp == Dest.A:
        comp = Comp.A
    elif comp == Dest.D:
        comp = Comp.D
    elif comp == Dest.M:
        comp = Comp.M
    
    return CInsn(dest,comp,jmp)

def dest_add(self,rhs):
    if self == Dest.D and rhs == Dest.M:
        return Comp.ADD_DM
    elif self == Dest.D and rhs == Dest.A:
        return Comp.ADD_DA
    elif self == Dest.D and rhs == Dest.M:
        return Comp.ADD_DM
    elif self == D and rhs == 1:
        return Comp.INCD
    elif self == A and rhs == 1:
        return Comp.INCA
    if self == M and rhs == 1:
        return Comp.INCM
Dest.__add__ = dest_add
def dest_sub(self,rhs):
    if self == Dest.D and rhs == Dest.M:
        return Comp.SUB_DM
    elif self == Dest.D and rhs == Dest.A:
        return Comp.SUB_DA
    elif self == Dest.D and rhs == Dest.M:
        return Comp.SUB_DM
    elif self == D and rhs == 1:
        return Comp.DECD
    elif self == A and rhs == 1:
        return Comp.DECA
    if self == M and rhs == 1:
        return Comp.DECM
Dest.__sub__ = dest_sub

We can then use this to verify two example programs from the slides.

from hack import *

A = Dest.A
D = Dest.D
M = Dest.M

prog = [
    At(R0),
    C(D, M),
    At(R1),
    C( D, D + M),
    At(17),
    C(D, D + A),
    At(R2),
    C( M, D)]
End = len(prog)
prog += [
    At(End),
    C( Dest.NULL, 0, Jump.JMP),
]

s = SolverFor("HORN")
s.add(horn(prog))
A, D, PC, A1, D1, PC1 = BitVecs("A D PC A1 D1 PC1", BV16)
s.add(assert_(Implies(PC == 8, MEM[R2] == MEM[R1] + MEM[R0] + 17)))
status = s.check()
print(status)
if status == sat:
    print(s.model())

This returns SAT, with a model.

The signum example

from hack import *
A = Dest.A
D = Dest.D
M = Dest.M


Pos = 8
End = 10
signum = [
    At(R0),
    C(D,M),
    At(Pos),
    C(Dest.NULL, D, Jump.JGE),
    At(R1),
    C(M,-1),
    At(End),
    C(Dest.NULL,0,Jump.JMP),
]
assert Pos == len(signum)
signum += [
    At(R1),
    C(M,1)
]
assert End == len(signum)
signum += [
    At(End),
    C(Dest.NULL,0,Jump.JMP)
]


s = SolverFor("HORN")
s.add(horn(signum))
A, D, PC, A1, D1, PC1 = BitVecs("A D PC A1 D1 PC1", BV16)
s.add(assert_(Implies(PC == End, If(MEM[R0] >= 0, MEM[R1] == 1, MEM[R1] == -1))))
print(s)
status = s.check()
print(status)
if status == sat:
    print(s.model())

Bits and Bobbles

This may not scale at all. These are both pretty simple programs.

However it would be interesting to attempt to go as far as one can or build a model of the stack based virtual machine and show that the compilation is a “simulation”. A form of relational verification.

I am not feeling python very much anymore. I’ve lost touch with reality.

Compare and contrast with coq

Try to help solver by partially giving invariants. Do this by replacing Insn with metalevel Insn that is uninterpreted anded with known invariants. Will Z3 accept this?

Other CHC verifiers of interest:

SeaHorn
JayHorn
GhiHorn

There are obvious blocks we can handle. “Larger” scale CHC translation can be done if you have a Control flow graph. Verifying that the CFG lifted version is identical to the unlifted version is interesting and useful too. This is a form of control flow integrity.