Oh cursed equation! How you haunt me!

I’ve been working on mechanizing equational reasoning for categories for a while now with not so much success.

The Egg paper came out and was very compelling to me. It is an implementation with novel twists of egraphs, a useful data structure for equational reasoning. I tried my hand at implementing the egraph data structure here with the purpose of using it for Catlab reasoning in mind.

But Alessandro Cheli has come along and really taken things to the next level with his Metatheory.jl library. The package includes a significantly improved egraph implementation, plus a classical rewriting system. It also has some really interesting ideas in regards to homoiconicity and theory composition. Maybe it’s useful to you. Check it out.

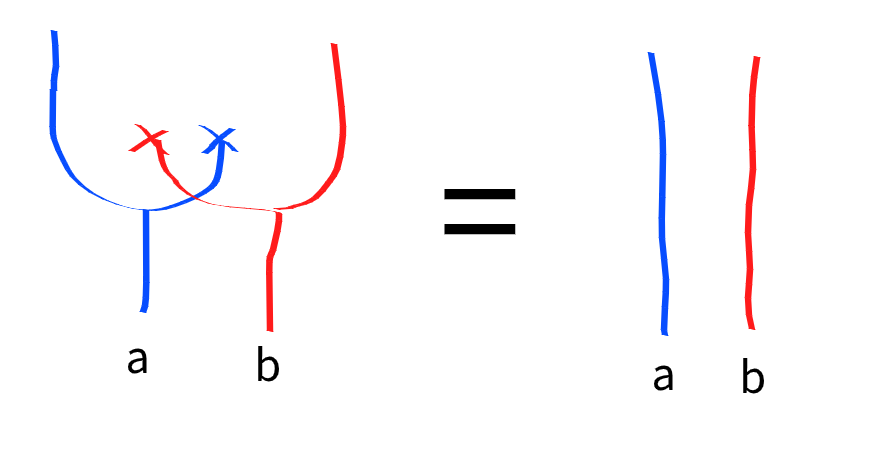
The equational reasoning that occurs in Catlab is compelling because it feels like high school algebra, but describes significantly more powerful systems of reasoning. It also has a beautiful and intuitive diagrammatic interpretation.

Understanding how to take a system like egraph rewriting, which in examples seems at the moment best suited for rewriting ordinary algebraic expressions, and tweak it to work with the more complicated logic of Catlab has been a challenge.

There are a couple problems.

  1. The typing context contains important information. Consider the rule $f \rightarrow id(a) \cdot f $. Looking at only the syntax of this rule, a is invented on the right hand side. This information actually comes from the type of f::hom(a,b)
  2. We need to strip off overloading? $\otimes$ is a symbol used in catlab for both the binary operator on objects and morphisms, as is customary. I guess this might fine? It makes me squeamish.
  3. Some rules require guarding on the type before execution. For most of the rules in Catlab, if the left hand side of the rule is well-typed, then so is the right. This is not the case in general though. Consider the trick question: Can you apply the interchange law (f ⊗ g) ⋅ (h ⊗ k) => (f ⋅ h) ⊗ (g ⋅ k) to the term (f ⊗ id(a)) ⋅ (id(b) ⊗ k)? No you can’t. For in my example, I have secretly decided that f actually has type b ⊗ c -> b ⊗ c and k has type c ⊗ a -> c ⊗ a. The other direction is always fine though. Given (f ⋅ h) ⊗ (g ⋅ k) is well typed, so is (f ⊗ g) ⋅ (h ⊗ k)

I thought way back that the types could be stripped and everything would be fine, like if you strip the types from the simply typed lambda calculus. This is not the case. I think this misconception is due to my inexperience doing hand calculations of this type (which almost no one does. String diagrams rule), plus I think you “code the happy path” when doing it by hand and may not even notice a situation where just shallow pattern matching on the syntax would allow you do do something verboten, since you’re smart enough to not make that dumb mistake.

My initial thinking this time around was to take a type tagging approach https://people.mpi-inf.mpg.de/~jblanche/mono-trans.pdf. This is a standard way of encoding more sophisticated typed logics into simpler typed ones. Type tagging replaces every term ever used with a more complex term that contains the type. In a curious analogy, it is the analog of dynamic typing vs static typing. In dynamically typed languages, all values carry with them tags describing which type they are at runtime.

As an example, the identity id(a) could be tagged as type(id(type(a,ob)), hom(typ(a,ob), type(a,ob))) or as hom(id(ob(a)), ob(a), ob(a)). You can see how verbose this is. It is not ideal both because it is unacceptable to write by hand, and because this extra structure is just more junk to choke your solver. But you can see that now the necessary types to fill in missing pieces of the right hand side is always available.

I tried this through some arcane metaprogramming methods involving Julog and it seemed too slow. Alessandro and James Fairbanks have a more elegant looking version of this here.

It feels insane that you need all this overhead when it is not necessary when working by hand. Many of the rules do not have this rhs invention problem or the typed guarding requirement. For cartesian categories, only about 5 of 30 rules have this condition. $(f \cdot g) \cdot h \rightarrow (f \cdot g) \cdot h$ is totally fine for example.

So here is idea 1, replace any new derived information on the right hand side with “function calls” that find that information. For our example, this becomes f => id(dom(type(f))) ⋅ f. Then we need to internalize the typing rules into the rewrite system

typing_rules = @theory begin
    dom(hom(a,b)) => a
    cod(hom(a,b)) => b
    type(id(a)) => hom(a,a)
    type(f ⋅ g) => hom( dom(type(f)) , cod(type(g)) )
    type(f ⊗ₘ g) => hom( dom(type(f)) ⊗ₒ dom(type(g)) , cod(type(f)) ⊗ₒ cod(type(g)))
    type(a ⊗ₒ b) => :ob
    type(munit()) => :ob
    type(σ(a,b)) => hom(a ⊗ₒ b, b ⊗ₒ a)
    type(⋄(a)) => hom(a, munit())
    type(Δ(a)) => hom(a, a ⊗ₒ a)
    type(pair(f,g)) => hom(dom(type(f)), cod(type(f)) ⊗ₒ cod(type(g)))
    type(proj1(a,b)) => hom(a ⊗ₒ b, a)
    type(proj2(a,b)) => hom(a ⊗ₒ b, b)
end

Idea two is to use Metatheory “guards” to enforce type correctness of the left hand side before a rule can fire. As part of this, the necessary type queries are added to the egraph. Alessandro had this idea of just returning the original expression to enforce a guard, which I think is pretty clever. Here is how I think the guard works for the interchange law. This will be cleaner with an upcoming Metatheory macro.

    (f ⊗ₘ p) ⋅ (g ⊗ₘ q) |>
    # future metatheory macros will clean this up
    begin
        fcod = addexpr!(_egraph, :(cod(type($f))))
        gdom = addexpr!(_egraph, :(dom(type($g))))
        pcod = addexpr!(_egraph, :(cod(type($p))))
        qdom = addexpr!(_egraph, :(dom(type($q))))
        if (fcod == gdom && pcod == qdom)
            :(($f ⋅ $g) ⊗ₘ ($p ⋅ $q))
        else
            :(($f ⊗ₘ $p) ⋅ ($g ⊗ₘ $q))
        end
    end

You can see that even making the query about whether the types are right adds them to the egraph. It may be currently unknown what the types are, but by adding them, eventually the typing rules will fire and this rule will have its chance again. This also isn’t as bad as it may appear performance wise, because the egraph in a sense memoizes these typing calls. See the Fibonacci example by Mason Protter which has non exponential complexity despite the naive implementation https://github.com/0x0f0f0f/Metatheory.jl/blob/master/test/test_fibonacci.jl

It is my belief that both of these points (internalization of the typing rules and guards) can be mechanized to produce a sound rule system for an arbitrary GAT. I could easily be wrong. The rough picture I suggest is that you need to infer by looking at the lhs of each rule what typing constraints are implied. If you do not imply the entire typing context, you need to add as many extra guards to ensure it as needed. For example, the well typed-ness of (f ⊗ₘ p) ⋅ (g ⊗ₘ q) implies $cod(f) \otimes cod(p) = dom(g) \otimes dom(q)$ but this does not imply the condition $cod(f) = dom(g) \land cod(p) = dom(q)$ so they must be added.

EGraphs are confusing to reason about. But 2 points:

  1. I think it is important that the Egraph inductively contains only well typed terms in some sense. This should be definable and checkable in a precise manner.
  2. I think it is important to have a semantic model in mind when working with egraphs. Pure syntax considerations lead you astray. EGraphs are more than just a bag of terms.

Here is a full script to run the derivation pair(proj1(a,b),proj2(a,b)) = id(a ⊗ₒ b). I can’t get it to go end to end without assistance yet. We’ll get there. I believe. The real holy grail is not proofs, but simplifications. This also works, but not yet at the depth I’m hoping for.

Evan Patterson’s explanation of the proof has been absolutely vital https://julialang.zulipchat.com/#narrow/stream/230248-catlab.2Ejl/topic/Automatic.20Theorem.20Proving/near/211396362. Zulip is nice for this.

using Pkg
Pkg.activate("metacat")
Pkg.add(url = "https://github.com/0x0f0f0f/Metatheory.jl.git")
using Metatheory
using Metatheory.EGraphs
using Metatheory.Util

# See this link for the catlab axioms
# https://github.com/AlgebraicJulia/Catlab.jl/blob/ce2fde9c63a8aab65cf2a7697f43cd24e5e00b3a/src/theories/Monoidal.jl#L127

cat_rules = @theory begin
    f ⋅ id(b) => f
    id(a) ⋅ f => f

    #f => f ⋅ id(dom(type(f)))
    #f => id(cod(type(f))) ⋅ f

    a ⊗ₒ munit() => a
    munit() ⊗ₒ a => a

    #a => a ⊗ₒ munit() 
    #a => munit() ⊗ₒ a

    f ⋅ (g ⋅ h) == (f ⋅ g) ⋅ h


end

monoidal_rules = @theory begin
    id(munit()) ⊗ₘ f => f
    f ⊗ₘ id(munit()) => f
    a ⊗ₒ (b ⊗ₒ c) == (a ⊗ₒ b) ⊗ₒ c
    f ⊗ₘ (h ⊗ₘ j) == (f ⊗ₘ h) ⊗ₘ j
    id(a ⊗ₒ b) == id(a) ⊗ₘ id(b)

    (f ⊗ₘ p) ⋅ (g ⊗ₘ q) |>
    # future metatheory macros will clean this up
    begin
        fcod = addexpr!(_egraph, :(cod(type($f))))
        gdom = addexpr!(_egraph, :(dom(type($g))))
        pcod = addexpr!(_egraph, :(cod(type($p))))
        qdom = addexpr!(_egraph, :(dom(type($q))))
        if (fcod == gdom && pcod == qdom)
            :(($f ⋅ $g) ⊗ₘ ($p ⋅ $q))
        else
            :(($f ⊗ₘ $p) ⋅ ($g ⊗ₘ $q))
        end
    end

    (f ⋅ g) ⊗ₘ (p ⋅ q) => (f ⊗ₘ p) ⋅ (g ⊗ₘ q)
end



sym_rules = @theory begin
    σ(a, b) ⋅ σ(b, a) == id(a ⊗ₒ b)
    (σ(a, b) ⊗ₘ id(c)) ⋅ (id(b) ⊗ₘ σ(a, c)) == σ(a, b ⊗ₒ c)
    (id(a) ⊗ₘ σ(b, c)) ⋅ (σ(a, c) ⊗ₘ id(b)) == σ(a ⊗ₒ b, c)

    (f ⊗ₘ h) ⋅ σ(a, b) |> begin
        fcod = addexpr!(_egraph, :(cod(type($f)))).id
        hcod = addexpr!(_egraph, :(cod(type($h)))).id
        if fcod == a && hcod == b
            :(σ(dom(type($f)), dom(type($h))) ⋅ ($h ⊗ₘ $f))
        else
            :(($f ⊗ₘ $h) ⋅ σ($a, $b))
        end
    end


    σ(c, d) ⋅ (h ⊗ₘ f) |> begin
        fdom = addexpr!(_egraph, :(dom(type($f)))).id
        hdom = addexpr!(_egraph, :(dom(type($h)))).id
        if fdom == c && hdom == d
            :(($f ⊗ₘ $h) ⋅ σ(cod(type($f)), cod(type($h))))
        else
            :(σ($c, $d) ⋅ ($h ⊗ₘ $f))
        end
    end

    # these rules arer not catlab
    σ(a, munit()) == id(a)
    σ(munit(), a) == id(a)
    σ(munit(), munit()) => id(munit() ⊗ₒ munit())

end



diag_rules = @theory begin

    Δ(a) ⋅ (⋄(a) ⊗ₘ id(a)) == id(a)
    Δ(a) ⋅ (id(a) ⊗ₘ ⋄(a)) == id(a)
    Δ(a) ⋅ σ(a, a) == Δ(a)

    (Δ(a) ⊗ₘ Δ(b)) ⋅ (id(a) ⊗ₘ σ(a, b) ⊗ₘ id(b)) == Δ(a ⊗ₒ b)


    Δ(a) ⋅ (Δ(a) ⊗ₘ id(a)) == Δ(a) ⋅ (id(a) ⊗ₘ Δ(a))
    ⋄(a ⊗ₒ b) == ⋄(a) ⊗ₘ ⋄(b)

    Δ(munit()) == id(munit())
    ⋄(munit()) == id(munit())
end


cart_rules = @theory begin

    Δ(a) ⋅ (f ⊗ₘ k) |> begin
        a_id = find(_egraph, a)
        if (
            addexpr!(_egraph, :(dom(type($f)))).id == a_id &&
            addexpr!(_egraph, :(dom(type($k)))).id == a_id
        )
            :(pair($f, $k))
        else
            :(Δ($a) ⋅ ($f ⊗ₘ $k))
        end
    end


    pair(f, k) => Δ(dom(type(f))) ⋅ (f ⊗ₘ k)
    proj1(a, b) == id(a) ⊗ₘ ⋄(b)
    proj2(a, b) == ⋄(a) ⊗ₘ id(b)
    f ⋅ ⋄(b) => ⋄(dom(type(f)))
    # Has to invent f. Hard to fix.
    # ⋄(b) => f ⋅ ⋄(b)  

    f ⋅ Δ(b) => Δ(dom(type(f))) ⋅ (f ⊗ₘ f)
    Δ(a) ⋅ (f ⊗ₘ f) => f ⋅ Δ(cod(type(f)))
end





typing_rules = @theory begin
    dom(hom(a, b)) => a
    cod(hom(a, b)) => b
    type(id(a)) => hom(a, a)
    type(f ⋅ g) => hom(dom(type(f)), cod(type(g)))
    type(f ⊗ₘ g) => hom(dom(type(f)) ⊗ₒ dom(type(g)), cod(type(f)) ⊗ₒ cod(type(g)))
    type(a ⊗ₒ b) => :ob
    type(munit()) => :ob
    type(σ(a, b)) => hom(a ⊗ₒ b, b ⊗ₒ a)
    type(⋄(a)) => hom(a, munit())
    type(Δ(a)) => hom(a, a ⊗ₒ a)
    type(pair(f, g)) => hom(dom(type(f)), cod(type(f)) ⊗ₒ cod(type(g)))
    type(proj1(a, b)) => hom(a ⊗ₒ b, a)
    type(proj2(a, b)) => hom(a ⊗ₒ b, b)
end


rules = typing_rules ∪ cat_rules ∪ monoidal_rules ∪ sym_rules ∪ diag_rules ∪ cart_rules ∪ typing_rules


# A goofy little helper macro
# Taking inspiration from Lean/Dafny/Agda
macro calc(e...)
    theory = eval(e[1])
    e = rmlines(e[2])
    @assert e.head == :block
    for (a, b) in zip(e.args[1:end-1], e.args[2:end])
        println(a, " =? ", b)
        @time println(areequal(theory, a, b; timeout = 40))
    end
end

# Get the Julia motor hummin'
@calc rules begin

    ((⋄(a) ⊗ₘ ⋄(b)) ⋅ σ(munit(), munit()))
    (σ(a, b) ⋅ (⋄(b) ⊗ₘ ⋄(a)))

end 


@calc rules begin
    id(a ⊗ₒ b)
    id(a) ⊗ₘ id(b)
    (Δ(a) ⋅ (id(a) ⊗ₘ ⋄(a))) ⊗ₘ id(b)
    (Δ(a) ⋅ (id(a) ⊗ₘ ⋄(a))) ⊗ₘ (Δ(b) ⋅ (⋄(b) ⊗ₘ id(b)))
    (Δ(a) ⊗ₘ Δ(b)) ⋅ ((id(a) ⊗ₘ ⋄(a)) ⊗ₘ (⋄(b) ⊗ₘ id(b)))
    (Δ(a) ⊗ₘ Δ(b)) ⋅ (id(a) ⊗ₘ (⋄(a) ⊗ₘ ⋄(b)) ⊗ₘ id(b))
    (Δ(a) ⊗ₘ Δ(b)) ⋅ (id(a) ⊗ₘ ((⋄(a) ⊗ₘ ⋄(b)) ⋅ σ(munit(), munit())) ⊗ₘ id(b))
    (Δ(a) ⊗ₘ Δ(b)) ⋅ ((id(a) ⊗ₘ (σ(a, b) ⋅ (⋄(b) ⊗ₘ ⋄(a))) ⊗ₘ id(b)))
    (Δ(a) ⊗ₘ Δ(b)) ⋅ ((id(a) ⊗ₘ (σ(a, b) ⋅ (⋄(b) ⊗ₘ ⋄(a))) ⊗ₘ id(b)))
    (Δ(a) ⊗ₘ Δ(b)) ⋅ ((id(a) ⋅ id(a)) ⊗ₘ (σ(a, b) ⋅ (⋄(b) ⊗ₘ ⋄(a))) ⊗ₘ id(b))
    (Δ(a) ⊗ₘ Δ(b)) ⋅ ((id(a) ⊗ₘ σ(a, b) ⊗ₘ id(b)) ⋅ (id(a) ⊗ₘ (⋄(b) ⊗ₘ ⋄(a)) ⊗ₘ id(b)))
    Δ(a ⊗ₒ b) ⋅ (id(a) ⊗ₘ (⋄(b) ⊗ₘ ⋄(a)) ⊗ₘ id(b))
    Δ(a ⊗ₒ b) ⋅ (id(a) ⊗ₘ (⋄(b) ⊗ₘ ⋄(a)) ⊗ₘ id(b))
    Δ(a ⊗ₒ b) ⋅ (proj1(a, b) ⊗ₘ proj2(a, b))
    pair(proj1(a, b), proj2(a, b))
end

# shorter proof also accepted
@calc rules begin
    id(a ⊗ₒ b)
    (Δ(a) ⊗ₘ Δ(b)) ⋅ ((id(a) ⊗ₘ (σ(a, b) ⋅ (⋄(b) ⊗ₘ ⋄(a))) ⊗ₘ id(b)))
    pair(proj1(a, b), proj2(a, b))
end

Where to go from here

  • We could just say this is already nice and push forward.
  • You may have noticed I have a few rules commented out. These may or may not present extra difficulties. The unit production rules are probably fine with another kind of guard. The deletion rule in the other direction will never be fine. This rule truly invents f in an essential way.
  • This is all totally unintegrated with catlab itself. A WIP. There are different directions one could go on this. Alessandro has a branch of Metatheory in the work for custom user defined data structures, so it is possible to use Catlab’s native GATExpr maybe. He’s looking for help too btw!
  • I’m kind of intrigued at trying to make a pure egg version of the above, especially so I can compile to wasm -String diagrams https://julialang.zulipchat.com/#narrow/stream/230248-catlab.2Ejl/topic/Using.20Metatheory.20for.20String.20Diagrams There is a compelling argument that string diagrams are a preferred representation, normalizing the associativity,commutative, and unit properties of a categorical construction. The useful canonicity of string diagrams is a viewpoint Evan Patterson has put forward. It has been suggested by Alessandro and others that generalizing the EGraph data structure in some sense may be to go. Extensions of the egraph that work natively on something more string diagram-like?
  • More wildly speculative. Co-end calculus? How to deal with binding forms? Daniele Palombi has brought up the coend calculus https://arxiv.org/pdf/1501.02503.pdf This seems like a very interesting application. I think the direct attack on this problem using Metatheory requires understanding how to deal with alpha equivalence in the EGraph Conversation here: https://julialang.zulipchat.com/#narrow/stream/277860-metatheory.2Ejl/topic/Formal.20Proofs.20for.20CT.3F. I personally would like to start attacking the problem from the angle of regular integrals and sums, which are syntactically analogous.
  • Proof Recording and output. The actual proof is there in the egraph rewriting process if we record it. Alessandro sounded interested in this direction and my understanding is it is also in the works for egg
  • Cody has also pointed out to me that he had a project with similar goals but different methods many moons ago https://github.com/codyroux/catnapp. I don’t think this got that far.