Keras and Learning Sine
One perspective on machine learning is that it is interpolation, curve fitting.
So I decided to try to fit sin(x) using a neural network.
Linear layers with Relu units will make piecewise linear curves.
It works, just not well.
Deep networks tend to get kind of hung up.
from keras.models import Sequential
model = Sequential()
from keras.layers.core import Dense, Activation
model.add(Dense(output_dim=5, input_dim=1))
model.add(Activation("relu"))
model.add(Dense(output_dim=5, input_dim=1))
model.add(Activation("relu"))
model.add(Dense(output_dim=5, input_dim=1))
model.add(Activation("relu"))
model.add(Dense(output_dim=5, input_dim=1))
model.add(Activation("relu"))
model.add(Dense(output_dim=1))
#Depth doesn't seem to work so well
#Wide seems better for this task.
#Of course what we're doing is incredibly stupid
model.compile(loss='mean_squared_error', optimizer='sgd')
import numpy as np
import matplotlib.pyplot as plt
x = np.linspace(-np.pi, np.pi, 100)
data = (np.random.random((100000))-.5) * 2 * np.pi
vals = np.sin(data)
model.fit(data, vals, nb_epoch=5, batch_size=32)
y = model.predict(x, batch_size=32, verbose=0)
plt.plot(x,y)
plt.plot(x,np.sin(x))
#plt.legend()
plt.show()
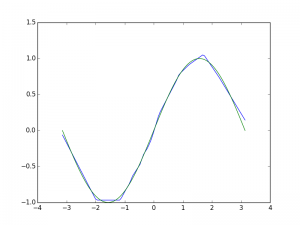
The final result is never all that great. Seems to have a lot of trouble at the minima and maxima of sine, probably because a relu is not a good model for what is happening at those points. And it takes a lot of iterations for the rest to look pretty good. Perhaps the optimizer needs more fine tuning. I have not looked within the box much at all. Maybe a more aggressive optimizer would converge faster for this very simple task.
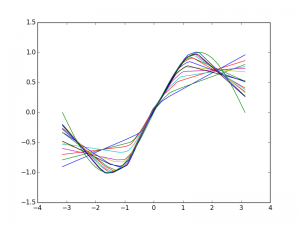
Here I plotted the result at intermediate steps of convergence. The accuracy tends to propagate out from 0 and sort of wrap around the curves. I wonder if this is due to where the thing is initialized
Still, I guess for being dead easy, not bad?