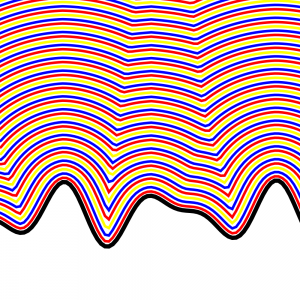
Elm, Eikonal, and Sol LeWitt
We saw this cool Sol LeWitt wall at MASS MoCA. It did not escape our attention that it was basically an eikonal equation and that the weird junctures were caustic lines.
It was drawn with alternating colored marker lines appearing a cm away from the previous line. This is basically Huygens principal.
So I hacked together a demo in elm. Elm is a Haskell-ish language for the web.

So I made a quick rip and run elm program to do this. This is the output, which I could make more dynamic.
The algorithm is to turn a list of points into their connecting lines. Then move the line perpendicular to itself, then recompute the new intersection points. It’s somewhat reminiscent of Verlet integration. Lines coordinates are momentum-like and points are position like and we alternate them. This is a finite difference version of the geometric Huygen’s principle.
Alternative methods which might work better include the Fast Marching Method or just using the wave equation and then plotting iso surfaces.
I also had to resample the function to get only the maximum y value for each x value in order to duplicate the LeWitt effect.
These are the helper functions with lots of junk in there
module LineHelpers exposing (..)
-- Maybe should just be doubles or nums
import Debug
fromJust : Maybe a -> a
fromJust x = case x of
Just y -> y
Nothing -> Debug.crash "error: fromJust Nothing"
toPointString : List (number, number) -> String
toPointString xs =
case xs of
(x,y) :: ys -> (toString x) ++ "," ++ (toString y) ++ " " ++ (toPointString ys)
_ -> ""
crossProd : (number,number,number) -> (number,number,number) -> (number,number,number)
crossProd (a,b,c) (d,e,f) = (b * f - c * e, c * d - a * f, a * e - b * d)
type alias PointListH number = List (number,number,number)
type alias LineListH number = List (number,number,number)
-- gives the mapping function the list and the list shifted by 1
neighbormap f a = let a_ = fromJust (List.tail a) in List.map2 f a a_
crossNeighbor = neighbormap crossProd
norm a b = sqrt (a * a + b * b)
shiftLine delta (a,b,c) = (a,b, (norm a b) * delta + c)
connectingLines = crossNeighbor
shiftLines delta = List.map (shiftLine delta)
intersections = crossNeighbor
-- nearly striaght lines will find their intersection at infinity.
-- maybe filter out a lower threshold on c
-- keep first and last point
last xs = let l = List.length xs in fromJust (List.head (List.drop (l - 1) xs))
timestep : Float -> List (Float,Float, Float) -> List (Float,Float, Float)
timestep delta points = let
firstpoint = fromJust (List.head points)
lastpoint = last points
connectlines = connectingLines points
newlines = shiftLines delta connectlines
newpoints = intersections newlines
filterednewpoints = List.filter (\(a,b,c) -> (abs c) > 0.01) newpoints
normpoints = List.map normalize filterednewpoints
result = firstpoint :: (normpoints ++ [lastpoint])
resample = List.map (maxfunc (List.map dehomogenize result)) initx
--result2 = removeoutoforder (-100000, 0,00) result
in List.map homogenize (zip initx resample)
homogenize (a,b) = (a,b,1)
dehomogenize (a,b,c) = (a / c, b / c)
normalize = dehomogenize >> homogenize
zip = List.map2 (,)
initx = List.map (toFloat >>((*) 4.5)) (List.range -200 400)
--inity = List.map (\x -> x * x / 50) initx
--inity = List.map (\x -> 300 + x * x / -50) initx
--inity = List.map (\x -> 25 * sin (x / 20) + 250) initx
inity = List.map (\x -> 25 * sin (x / 20) + 250 + 15 * sin (x/13)) initx
initxy = zip initx inity
initxyh = List.map homogenize initxy
iterate n f x = if n == 0 then [] else (f x) :: iterate (n - 1) f (f x)
paths = (List.map << List.map) dehomogenize (iterate 60 (timestep 5.0) initxyh)
colors = List.concat (List.repeat (List.length paths) ["red", "blue", "yellow"] )
removeoutoforder prev xs = case xs of
y :: ys -> if prev < y then (y :: removeoutoforder y ys) else removeoutoforder prev ys
_ -> []
neighborzip a = let a_ = fromJust (List.tail a) in zip a a_
linearinterp x ((x1,y1), (x2,y2)) = (y1 * (x2 - x) + y2 * (x - x1)) / (x2 - x1)
maxfunc : List (Float, Float) -> Float -> Float
maxfunc points x = let
pairs = neighborzip points
filterfunc ((x1,y1), (x2,y2)) = (xor (x < x1) (x < x2))
candidates = List.filter filterfunc pairs
yvals = List.map (linearinterp x) candidates in Maybe.withDefault 100 (List.maximum yvals)
And this is the svg main program.
import Html exposing (Html, button, div, text)
import Html.Events exposing (onClick)
import Svg exposing (..)
import Svg.Attributes exposing (..)
import LineHelpers exposing (..)
roundRect : Html.Html msg
roundRect =
svg
[ width "1000", height "1000",viewBox "-100 0 350 350" ]
(List.reverse ([--[ rect [ x "10", y "10", width "100", height "100", rx "15", ry "15" ] [],
-- polyline [ fill "none", stroke "red", points "20,100 40,60 70,80 100,20" ] [],
polyline [ fill "none", stroke "black", strokeWidth "5.0", points (LineHelpers.toPointString LineHelpers.initxy) ] []] ++
(List.map2 (\path color -> polyline [ fill "none", stroke color, strokeWidth "3.0", points (LineHelpers.toPointString path)] []) LineHelpers.paths LineHelpers.colors)))
main =
Html.beginnerProgram { model = model, view = view, update = update }
-- MODEL
type alias Model = Int
model : Model
model =
0
-- UPDATE
type Msg = Increment | Decrement
update : Msg -> Model -> Model
update msg model =
case msg of
Increment ->
model + 1
Decrement ->
model - 1
-- VIEW
view : Model -> Html Msg
view model =
div []
[ button [ onClick Decrement ] [ Html.text "-" ]
, div [] [ Html.text (toString model) ]
, button [ onClick Increment ] [ Html.text "+" ],
roundRect
]
notes on elm
elm is installed with npm
elm-repl
you import packages (including your own) with
import ThisPackage
and you check types by just writing them and hitting enter rather than :t
elm-live is a very handy thing. A live reloading server that watches for changes in your files.
elm-make myfile.elm
will generate the javascript and html
This is a good tutorial and a good snippet to get you going
Differences from Haskell:
elm isn’t lazy which is probably good.
The composition operator (.) is now «
elm doesn’t have the multiline pattern match of haskell. You need to use case expressions. I miss them.
typeclass facilities are not emphasized.
The list type is List a rather than [a]