Casadi - Pretty Damn Slick
Casadi is something I’ve been aware of and not really explored much. It is a C++ / python / matlab library for modelling optimization problems for optimal control with bindings to IPOpt and other solvers. It can produce C code and has differentiation stuff. See below for some examples after I ramble.
I’ve enjoyed cvxpy, but cvxpy is designed specifically for convex problems, of which many control problems are not.
Casadi gives you a nonlinear modelling language and easy access to IPOpt, an interior point solver that works pretty good (along with some other solvers, many of which are proprietary however).
While the documentation visually looks very slick I actually found it rather confusing in contents at first. I’m not sure why. Something is off.
You should download the “example pack” folder. Why they don’t have these in html on the webpage is insane to me. https://github.com/casadi/casadi/releases/download/3.4.4/casadi-example_pack-v3.4.4.zip
It also has a bunch of helper classes for DAE building and other things. They honestly really put me off. The documentation is confusing enough that I am not convinced they give you much.
The integrator classes give you access to external smart ode solvers from the Sundials suite. They give you good methods for difficult odes and dae (differential algebraic equations, which are ODEs with weird constraints like x^1 + y^1 == 1) Not clear to me if you can plug those in to an optimization, other than by a shooting method.
Casadi can also output C which is pretty cool.
I kind of wondered about Casadi vs Sympy. Sympy has lot’s of general purpose symbolic abilities. Symbolic solving, polynomial smarts, even some differential equation understanding. There might be big dividends to using it. But it is a little harder to get going. I feel like there is an empty space for a mathemtical modelling language that uses sympy as it’s underlying representation. I guess monkey patching sympy expressions into casadi expression might not be so hard. Sympy can also output fast C code. Sympy doesn’t really have any support for sparseness that I know of.
As a side note, It can be useful to put these other languages into numpy if you need extended reshaping abilities. The other languages often stop at matrices, which is odd to me.
Hmm. Casadi actually does have access to mixed integer programs via bonmin (and commercial solvers). That’s interesting. Check out lotka volterra minlp example
https://groups.google.com/forum/#!topic/casadi-users/8xCHmP7UmpI
The optim interface makes some of this look better. optim.minimize and subject_to. Yeah, this is more similar to the interfaces I’m used to. It avoids the manual unpacking of the solution and the funky feel of making everything into implicit == 0 expressions.
https://web.casadi.org/blog/opti/
Here is a simple harmonic oscillator example using the more raw casadi interface. x is positive, v is velocity, u is a control force. I’m using a very basic leap frog integration. You tend to have to stack things into a single vector with vertcat when building the final problem.
from casadi import *
import matplotlib.pyplot as plt
g = 9.8
N = 100
x = SX.sym('x',N)
v = SX.sym('v', N)
u = SX.sym('u', N-1)
#theta = SX('theta', N)
#thdot = SX('thetadot', N)
dt = 0.1
constraints = [x[0]-1, v[0]] # expressions that must be zero
for i in range(N-1):
constraints += [x[i+1] - (x[i] + dt * v[i]) ]
constraints += [v[i+1] - (v[i] - dt * x[i+1] + u[i] * dt)]
cost = sum([x[i]*x[i] for i in range(N)]) + sum([u[i]*u[i] for i in range(N-1)])
nlp = {'x':vertcat(x,v,u), 'f':cost, 'g':vertcat(*constraints)}
S = nlpsol('S', 'ipopt', nlp)
r = S(lbg=0, ubg=0) # can also give initial solutiuon hint, some other things
x_opt = r['x']
x = x_opt[:N]
v = x_opt[N:2*N]
u = x_opt[2*N:]
#u_opt = r['u']
print('x_opt: ', x_opt)
print(S)
plt.plot(x)
plt.plot(u)
plt.plot(v)
plt.show()
Let’s use the opti interface, which is pretty slick. Here is a basic cartpole https://web.casadi.org/blog/opti/
from casadi import *
import matplotlib.pyplot as plt
g = 9.8
N = 100
# https://web.casadi.org/blog/opti/
opti = casadi.Opti()
x = opti.variable(N)
v = opti.variable(N)
theta = opti.variable(N)
dtheta = opti.variable(N)
u = opti.variable(N-1)
opti.subject_to( u <= 1)
opti.subject_to( -1 <= u)
opti.subject_to( x <= 2)
opti.subject_to( -2 <= x)
opti.subject_to(x[0] == 0)
opti.subject_to(v[0] == 0)
opti.subject_to(theta[0] == 0)
opti.subject_to(dtheta[0] == 0)
dt = 0.05
for i in range(N-1):
opti.subject_to( x[i+1] == x[i] + dt * (v[i]))
opti.subject_to( v[i+1] == v[i] + dt * (x[i+1] + u[i]))
opti.subject_to( theta[i+1] == theta[i] + dt * (dtheta[i]))
opti.subject_to( dtheta[i+1] == dtheta[i] + dt * (u[i] * cos(theta[i+1]) - sin(theta[i+1]) ))
opti.minimize( sum1(sin(theta)))
opti.solver("ipopt") #,p_opts, s_opts)
sol = opti.solve()
print(sol.value(x))
plt.plot(sol.value(x), label="x")
plt.plot(sol.value(u), label="u")
plt.plot(sol.value(theta), label="theta")
plt.legend()
plt.show()
'''
p = opti.parameter()
opti.set_value(p, 3)
'''
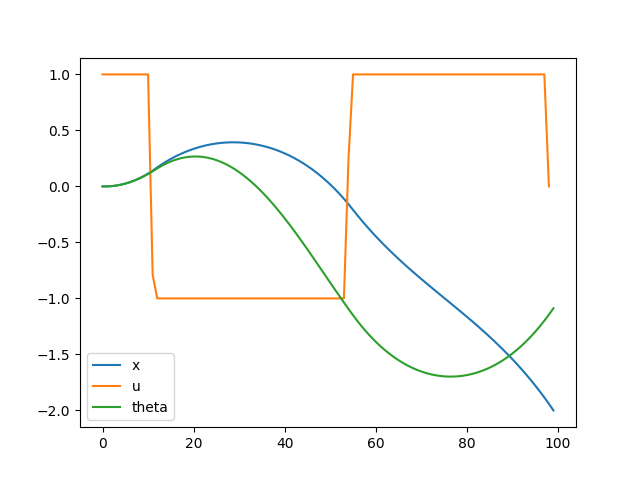
Very fast. Very impressive. Relatively readable code. I busted this out in like 15 minutes. IPopt solves the thing in the blink of an eye (about 0.05s self reported). Might be even faster if I warm start it with a good solution, as I would in online control (which may be feasible at this speed). Can add the initial condition as a parameter to the problem
I should try this on an openai gym.
Haskell has bindings to casadi.