Sorting networks are a circuit flavored take on sorting. Although you can build circuits for any size input, any particular circuit works for a fixed sized input. They are like an unrolling of the loops or recursion of more familiar sorting algorithms. They come up also in the context of parallel and gpu sorting

Here’s an interesting thing. We can go to Wikipedia and get a little python snippet for the comparison order of a Batcher odd-even mergesort. Kind of a confusing algorithm. Why does it even work? Is it even right? It’s written in some kind of funky, indexful generator style.

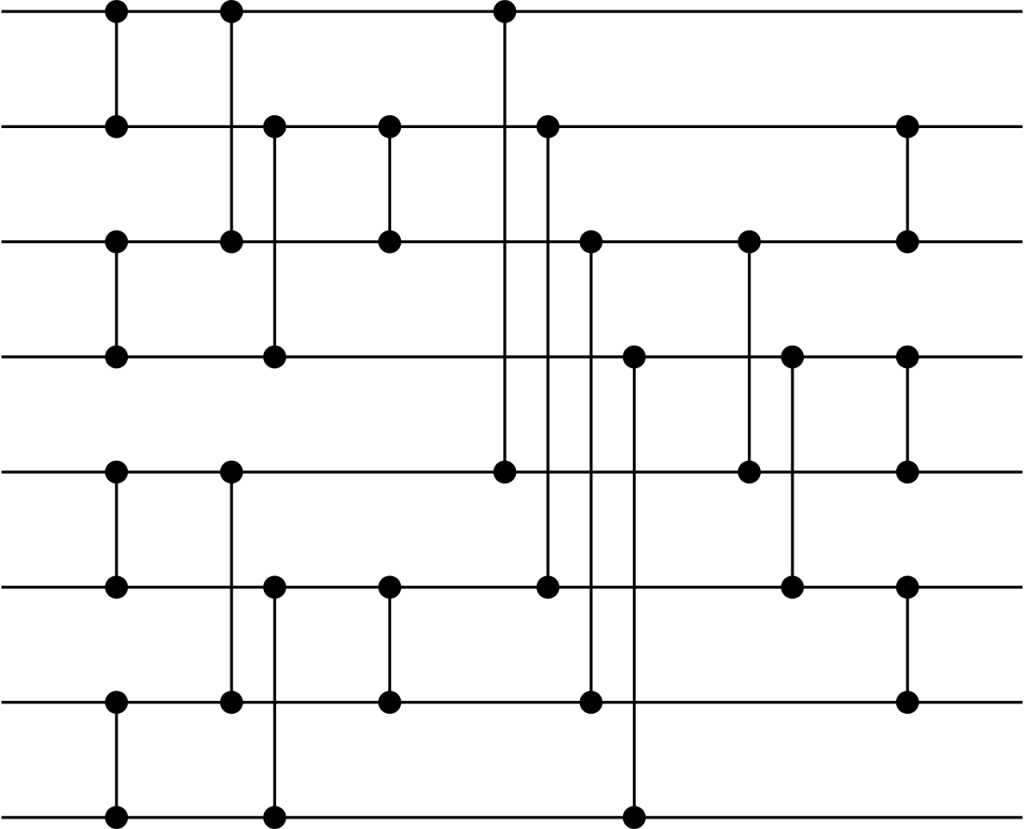Source: Wikipedia

#direct from https://en.wikipedia.org/wiki/Batcher_odd%E2%80%93even_mergesort
def oddeven_merge(lo: int, hi: int, r: int):
    step = r * 2
    if step < hi - lo:
        yield from oddeven_merge(lo, hi, step)
        yield from oddeven_merge(lo + r, hi, step)
        yield from [(i, i + r) for i in range(lo + r, hi - r, step)]
    else:
        yield (lo, lo + r)

def oddeven_merge_sort_range(lo: int, hi: int):
    """ sort the part of x with indices between lo and hi.

    Note: endpoints (lo and hi) are included.
    """
    if (hi - lo) >= 1:
        # if there is more than one element, split the input
        # down the middle and first sort the first and second
        # half, followed by merging them.
        mid = lo + ((hi - lo) // 2)
        yield from oddeven_merge_sort_range(lo, mid)
        yield from oddeven_merge_sort_range(mid + 1, hi)
        yield from oddeven_merge(lo, hi, 1)

def oddeven_merge_sort(length: int):
    """ "length" is the length of the list to be sorted.
    Returns a list of pairs of indices starting with 0 """
    yield from oddeven_merge_sort_range(0, length - 1)

def compare_and_swap(x, a, b) -> None:
    if x[a] > x[b]:
        x[a], x[b] = x[b], x[a]

Well we can confirm this relatively straightforwardly using z3 by replacing the implementation of compare_and_swap with its z3 equivalent. We then ask z3 .

def compare_and_swap_z3(x,y):
    x1, y2 = FreshInt(), FreshInt()
    c = If(x <= y, And(x1 == x, y1 == y) , And(x1 == y, y1 == x) )
    return x1, y1, c

N = 64 # size of sorting network

s = Solver()

a = [Int(f"x_{i}") for i in range(N)] #build initial array in z3 variables
pairs_to_compare = list(oddeven_merge_sort(N)) #get sequence of compare and swaps to use
a_orig = a.copy()
for i,j in pairs_to_compare:
   x = a[i]
   y = a[j]
   x1,y1,c = compare_and_swap_z3(x,y) 
   a[i] = x1
   a[j] = y1
   s.add(c)
    
def sorted_list(x): # list is sorted
    return And([x <= y for x,y in zip(x , x[1:])])

def in_list(x,a): # x is in the list of a
    return Or([x == y for y in a])
def sub_list(a, b): # all elements of a appear in b
    return And([in_list(x,a) for x in b ])
def same_elems(a,b): # a contains the same elements as b
    return And(sub_list(a,b), sub_list(b,a))

s.add(Not(And(sorted_pred(a), same_elems(a_orig,a) )))
s.check()

This comes back unsat, hence there are no inputs or executions that do not come back sorted. If I delete some elements from pair_to_compare, it comes back sat, showing that it doesn’t always sort.

The trick here is that the circuit is fixed size, so we have no need for induction, one of the main things z3 is rather finicky at.

It’s somewhat interesting to note that the output of odd_even_merge is a sequence of instructions, we can think of this as interpreting a very small 1 instruction programming language.

We can also confirm similarly a simple odd-even bubblesort and other similar algorithms.

def even_comp(l):
    for x in [(i, i + 1) for i in range(0,l-1,2)]:
        yield x
def odd_comp(l):
    for x in [(i, i + 1) for i in range(1,l-1,2)]:
        yield x
def even_odd(l, n):
    for j in range(n):
        for x in even_comp(l):
            yield x
        for x in odd_comp(l):
            yield x
            
def bubble(l):
    for x in even_odd(l,l//2):
        yield x

Q: What about using uninterpreted sorts rather than integers? Integers is pretty convincing to me.

same_elems is slightly weaker than a permutation predicate. Wasn’t super obvious to me the best way to do a permutation predicate in z3. Would I want to internalize the array?

Edit: Upon further thought, actually the sort IS a nice predicate for permutation. How do we compute if two things are permutations of each other? By sorting them and forcing a zipped equality. Alternatively count the number of each element (a piece of bucket sort). Since this sort is done by composing swaps, it is somewhat intrinsically a permutation

As a bummer though, I think randomized testing on arrays would be equally or perhaps more convincing of the correctness of the algorithm. Oh well.