You can make egraphs support stream like things / rational terms.

The basic gist is to mix together automata minimization https://www.philipzucker.com/naive_automata/ in with the egraph so as to be able to support infinite streams. This is by adding a cofunction/observation table dict[Eid, Obs] and implementing co-merging during rebuilding.

Considering such things, other interesting little side notes fall out such as an intriguing way of writing unification.

The problem with streams in Egraphs

The egg diagram is kind of a lie.

The egg diagram draws an egraph as enodes which have children that are eclasses represented as a dotted boundary around other enodes. This can also be thought of as a bipartite graph between eclasses and enodes.

LIES

If you only build egraphs via the process of inserting well founded terms and asserting equalities, you can not build the following egraph:

Spiritually this egraph represents the singleton set of the infinite term { f(f(f(f(f(f(...)))))) }

You can build this closely related but not identical graph

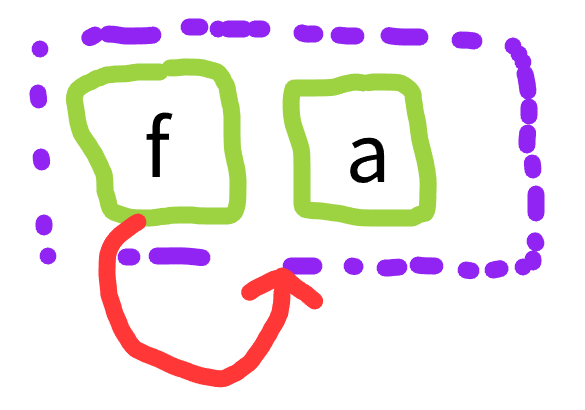
which represents the infinite set of finite terms {a, f(a), f(f(a)), f(f(f(a))), ...}. You can build it by

  1. insert term a
  2. insert term f(a)
  3. union a and f(a)

This is kind of what we tend to use as a stand-in for the infinite term above. It has the problem though that if we really intend the infinite term, as we do in streams, then a is junk. And if we build the same thing twice with different names, they won’t be merged

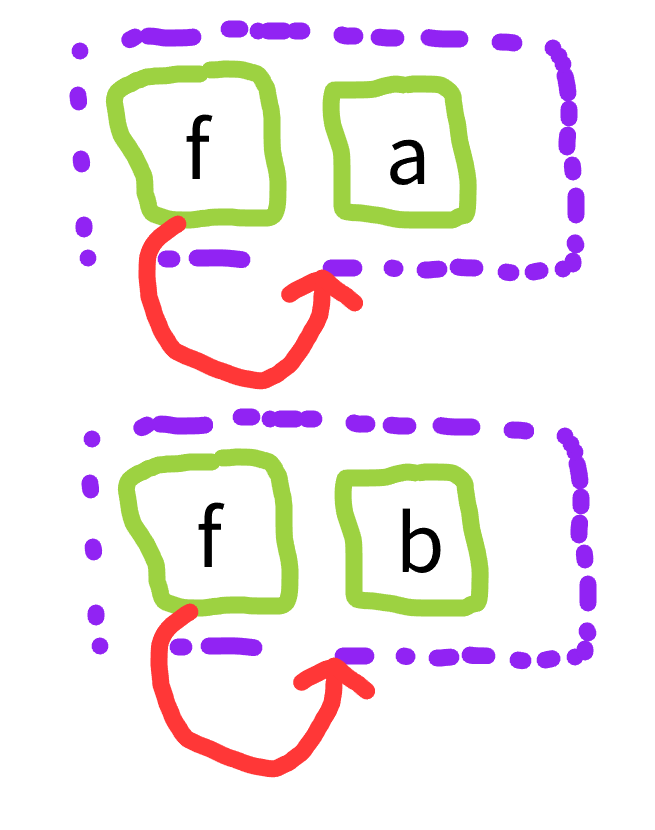
This isn’t persay a total show stopper, but it is a simple inelegance that leaks declarativity. And leaking such things on such simple examples means you’re going to get more and more ensnarled on more complex examples.

Even if you could build the impossible egraph by reaching in an tweaking the underlying structures or raw makeset capabilities, congruence closure / rebuilding will not notice and compactify these two obviously equal structures.

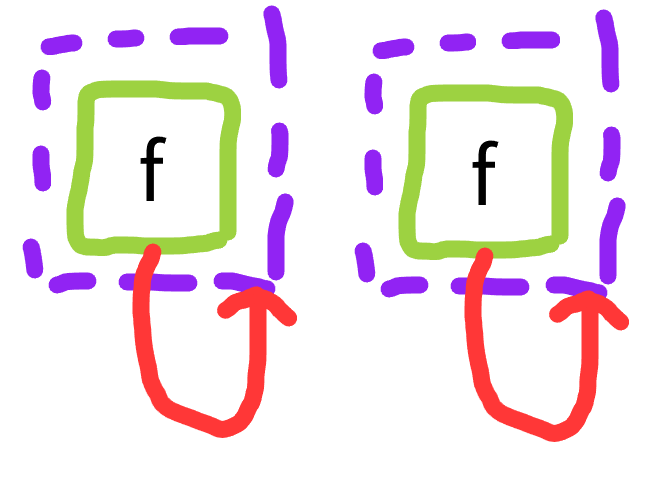
This is reminiscent of the alpha renaming problem that \x. x and \y. y should be the same. And in fact the two problems are a bit inter-modellable which is interesting. If you have alpha renameable lambdas, you can use a fix constructor to model these loops. And you can use rational terms to refer back to binding sites instead of using names, which is an intrinsic alpha invariant form.

This situation occurs when we wish to discuss and manipulate stream like [0,0,0,0,0,0,...]

zerostream = Cons(0, zerostream)

or [1,0,1,0,1,0,...]

zeroone = Cons(0, onezero)
onezero = Cons(1, zeroone)

We can choose to define a constant zerostream and tie the knot using union, but we won’t notice if we define again

zerostream = Cons(0, zerostream)
zerostream' = Cons(0, zerostream')
zerostream'' = Cons(0, zerostream)

Or we won’t notice if the equality process determines a new nontrivial fact that makes the streams equal. For example a stream [a + b, a + b, a + b, ...] and stream [b + a, b + a, b + a, ...] should end up compacted once we union(a+b, b+a), but the well founded egraph can’t discover this.

abstream = Cons(a + b, abstream)
bastream = Cons(b + a, bastream)
union(a + b, b + a)

In turn, PEGs https://rosstate.org/publications/eqsat/, one possible approach to implementing compiler IRs inside egraphs is essentially representing blocks as streams of their iterations.

Automata Minimization

The typical sense that these streams are equivalent is that they observationally equivalent and they can be compacted via automata minimization.

Last time, I described how naive automata minimization works https://www.philipzucker.com/naive_automata/ . The key point is that states are only meaningfully distinct if they have distinct observations. We can operationalize this as a dictionary dict[stateid, Obs] and compress the dictionary in a simple loop, iteratively refining a partition of the state ids into a coarsest partition that cannot be observationally split.

If you’re entrenched in such things, this is reminiscent of the process of egraph rebuilding. This was noted in the tree automata analogy work, more on that later.

Automata minimization can be used as the analog of hash consing for rational loopy data structures.

Egraphs themselves are “just” a hashcons++, a hash cons mixed with a union find. They are represented as the combination of a table dict[ENode, Eid] and a unionfind. This table tells us how to evaluate expressions in the current model. It is very much the analog of a table saying how to perform multiplication in a finite group add_mod2 = {(1,0):1, (1,1):0, (0,0):0, (0,1):1}; inv_mod2 = {1 : 1, 0 : 0}; id_mod2 = {() : 0}.

Monotonicity: Everything needs to walk in the same direction

Equality saturation is monotonically discovering new well formed terms and increasing the equalities known (these equalities in turn shrink the data structure through compaction, but it’s best not to think about that from a semantic meaning perspective).

Here is the point that stumped me for a long time, as trivial as it will sound.

The direction of monotonicity that works for observations is that we can forget observations, make fewer and fewer distinctions. If we are “learning” new observations about state, we need to split two state that may already have been merged as equivalent by automata minimization. We could perhaps do this, but then state “equality” via minimization becomes meaningless as it can always end up being reversed, and we can’t compress away states.

The resolution of this conundrum is that the observation table has to be partial and that the keys that are not in the observation table are not unobserved, the are unexpanded. They are in fact maximally observed, as in they have unique identity. We may choose to “seal”/”close” a state at a later point, perhaps via a rule, saying it will have no more observations possible than those in the observation record.

If the observations include a term that will have new equalities discovered that’s fine. That does not constitute a disruption of the “sealing”. 1 -> Obs(a + b) and 2 -> Obs(b + a) but upon discovery of a + b = b + a, the two observations become equivalent and the two states can be seen to be equivalent.

In short, we can make a combined data structure consisting of an enodes table, a union find, and an observation table. I call this data structure a co-egraph. There is a pleasing symmetry/duality between enodes and obs.

from dataclasses import dataclass
import itertools

EId = int
ENode = tuple[str, tuple[EId, ...]]
Term = tuple[str, "Term", ...]
Obs = tuple[str, tuple[EId, ...]]

@dataclass
class EGraph:
    enodes: dict[ENode, EId]
    uf: list[EId]
    obs: dict[EId, Obs]

    def __init__(self):
        self.enodes = {}
        self.uf = []
        self.obs = {}

    # Typical Egraph Stuff
    def makeset(self) -> EId:
        """Create a new equivalence class"""
        x = len(self.uf)
        self.uf.append(x)
        return x

    def find(self, x: EId) -> EId:
        """Get canonical EId"""
        while x != self.uf[x]:
            x = self.uf[x]
        return x

    def union(self, x: EId, y: EId) -> EId:
        x = self.find(x)
        y = self.find(y)
        if x != y:
            self.uf[x] = y
        return y
    
    # New Co Egraph stuff
    def merge_obs(self, obs1, obs2): #comerge
        head1, args1 = obs1
        head2, args2 = obs2
        if head1 != head2 or len(args1) != len(args2):
            raise ValueError("Inconsistent observation")
        for a1, a2 in zip(args1, args2):
            self.union(a1,a2)
    
    def observe(self, x : EId, obs : Obs):
        x = self.find(x)
        obs1 = self.obs.get(x)
        if obs1 != None:
            self.merge_obs(obs1, obs)
        self.obs[x] = obs

    def rebuild(self):
        while True:
            # Automata minimization over observed keys. See blog post https://www.philipzucker.com/naive_automata/
            observed = list(self.obs.keys()) # only minimize over observed entitiies.
            partmap = {i : observed for i in observed}  # initial unrefined partition
            while True:
                newpartmap = {}
                z = {i: (head, tuple(partmap[x] if x in partmap else [x] for x in args)) for i, (head, args) in self.obs.items()}
                for _, equivs in itertools.groupby(sorted(observed, key=lambda state:z[state]), lambda state: z[state]):
                    equivs = list(equivs)
                    for i in equivs:
                        newpartmap[i] = equivs
                if newpartmap == partmap:
                    break
                partmap = newpartmap
            
            for part in partmap.values():
                for j in part:
                    self.union(j, part[0])

            # congruence closure. Typical egraph stuff
            newenodes = {}
            for k, v in self.enodes.items():
                # congruence closure
                (head, args) = k
                newk = (head, tuple(self.find(a) for a in args))
                v1 = self.enodes.get(newk)
                if v1 is not None:
                    self.union(v, v1)
                newenodes[newk] = self.find(v)

            # observation compaction and conflict resolution / co-merging.
            newobs = {}
            for v, obs in self.obs.items():
                # check for duplicated observations
                obs1 = self.obs.get(self.find(v))
                if obs1 != None:
                    self.merge_obs(obs1, obs)
                (head, args) = obs
                newargs = tuple(self.find(a) for a in args)
                newobs[self.find(v)] = (head, newargs)

            if newenodes == self.enodes and newobs == self.obs:
                break
            self.enodes = newenodes
            self.obs = newobs

    def add_term(self, t: Term) -> EId:
        head, *args = t
        args = tuple(self.add_term(arg) for arg in args)
        v = self.enodes.get((head, args))
        if v is None:
            v = self.makeset()
            self.enodes[(head, tuple(args))] = v
        return v

Ok, so we still have the usual egraph stuff.

E = EGraph()
fa = E.add_term(("f", ("a",)))
a = E.add_term(("a",))
print(E)
E.union(a, fa)

EGraph(enodes={('a', ()): 0, ('f', (0,)): 1}, uf=[0, 1], obs={})

But now I can build a loopy data structure and they will be compacted by rebuilding

E = EGraph()
x = E.makeset()
E.observe(x, ("f", (x,)))
E.rebuild()
print("added loopy f", E)
y = E.makeset()
E.observe(y, ("f", (y,)))
print("added second loopy f", E)
E.rebuild()
print("compacted away", E)
z = E.makeset()
E.observe(z, ("f", (x,))) # a slightly different duplication of x
E.rebuild()
E

EGraph(enodes={}, uf=[0, 0, 0], obs={0: ('f', (0,))})

Here is the [a + b, a + b, ...] [b + a, b + a, ....] example.

E = EGraph()
ab = E.add_term(("+", ("a"), ("b")))
ba = E.add_term(("+", ("b"), ("a")))
print(E)
# build abstream and bastream
abstream = E.makeset()
E.rebuild()
E.observe(abstream, ("cons", (ab,abstream)))
bastream = E.makeset()
E.observe(bastream, ("cons", (ba,bastream)))
E.rebuild()
# They aren't equal
assert E.find(abstream) != E.find(bastream)
E
# learn a + b = b + a
E.union(ab,ba)
E.rebuild()
# Now they are
assert E.find(abstream) == E.find(bastream)
E

EGraph(enodes={('a', ()): 0, ('b', ()): 1, ('+', (0, 1)): 3, ('+', (1, 0)): 3}, uf=[0, 1, 3, 3, 4, 4], obs={4: ('cons', (3, 4))})

Unification a la Egraphs

aka Extra Lazy Unification

aka Unification is Observational

This kind of surprising me when I noticed it. If you remove the enodes table from the above, you have a union find + observation table. This implements unification in a slightly unusual style.

Explicitly, there is no occurs check. We allow rational terms. I suggest that actually unification is naturally coalgebraic / observational. A unification variable is either unexpanded or it has an observation to a term constructor.

It is noted in particular in higher order unification that there are 3 different cases that occur in unification: rigid-rigid f(X) = f(Y), flex-rigid X = f(Y), flex-flex X = Y. These occur as cases inside regular first order unification also.

merge_obs deals with rigid-rigid, observe is flex-rigid, and union is called for flex-flex

It is strangely lazier than regular unification (which is already by design and purpose extremely lazy). When you union, merge_obs, or observe, it only resolves a single layer of unification and delays the rest until the next rebuild where it might find actual conflicts. This is reminiscent of how egg made congruence closure lazy compared to the classical algorithm to amoritize rebuilding.

I have left out the automata minimization thing here. It would only fire on fully grounded rational terms, since unexpanded unification variables are considered identifiable.

Perhaps you could build a minikanren around this data structure.

Both Yihong and I have noted and tried to use egglog to implement unification via injectivity rules Cons(x,xs) = Cons(y,ys) -> (x = y & x = xs). This works, but it is cute that unification is very built in vbecuse of other motivations by the coegraph approach

from dataclasses import dataclass
from typing import Any
@dataclass
class Unify():
    uf: list[int]
    obs: dict[int, tuple[Any, tuple[int]]]
    def __init__(self):
        self.uf = []
        self.obs = {}
    def make_var(self):
        v = len(self.uf)
        self.uf.append(v)
        return v
    def add_term(self, t):
        # try to check for rationality?
        if isinstance(t, int):
            return t
        head, *args = t
        args = tuple(self.add_term(arg) for arg in args)
        # we're not interning at all here, which is fine but inefficient.
        x = self.make_var() 
        self.observe(x, (head, args))
        return x
    def find(self, x):
        while self.uf[x] != x:
            x = self.uf[x]
        return x
    def union(self, x, y):
        x = self.find(x)
        y = self.find(y)
        self.uf[x] = y
        return y
    def merge_obs(self, obs, obs1): # unify_flat
        head, args = obs
        head1, args1 = obs1
        if head != head1:
            raise Exception("head mismatch")
        if len(args) != len(args1):
            raise Exception("arity mismatch")
        for a,a1 in zip(args, args1):
            self.union(a,a1)
    def observe(self, x, obs):
        x = self.find(x)
        o = self.obs.get(x)
        if o != None:
            self.merge_obs(o, obs)
        self.obs[x] = obs
    def extract(self,x):
        # assuming a well founded term. Could extract the rational term?
        x = self.find(x)
        f = self.obs.get(x)
        if f == None:
            return x
        else:
            head, args = f
            return (head, *[self.extract(a) for a in args])
    def rebuild(self):
        while True:
            newobs = {}
            # "unobserved" vars aren't be merged. unobserved is actually Maximally observed, i.e. has identity.
            for x,obs in self.obs.items():
                x1 = self.find(x)
                obs1 = self.obs.get(x1)
                if obs1 != None:
                    self.merge_obs(obs, obs1)
                (head, args) = obs
                newobs[x1] = (head, tuple(map(self.find, args)))
            if self.obs == newobs:
                break
            self.obs = newobs

U = Unify()
x = U.make_var()
y = U.make_var()
z = U.make_var()
print(U)
#U.union(x,y)
a_x = U.add_term(("a", ("b", z)))
b_y = U.add_term(("a", y))
U.union(a_x, b_y)
print(U)
U.rebuild()
print(U)
U.extract(a_x)

Unify(uf=[0, 1, 2], obs={})
Unify(uf=[0, 1, 2, 3, 5, 5], obs={3: ('b', (2,)), 4: ('a', (3,)), 5: ('a', (1,))})
Unify(uf=[0, 1, 2, 1, 5, 5], obs={1: ('b', (2,)), 5: ('a', (1,))})





('a', ('b', 2))

Rational Lambdas

If you have rational trees, there is kind of interesting knot tying available to achieve alpha equivalence.

If I represent the lambda \x. \y. x as ("lam", "x", ("lam", "y", ("var" , "x"))) this is a named representation and it isn’t intrinsic that it is the same thing as the renamed term ("lam", "z", ("lam", "y", ("var" , "z"))).

If you look at the graph form, a cute way of representing the variable is to just have it be a pointer back to it’s binding site. This for is intrinsically alpha invariant.

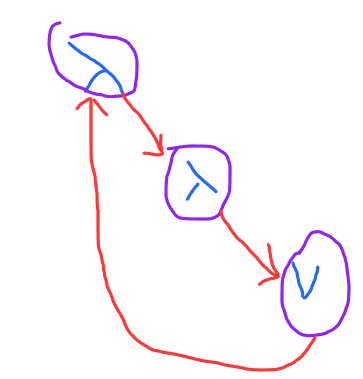
This is basically a rational tree. If you construct the same rational tree twice, automata minimization will discover the equivalence.

let expressions let x = 3 in x + 4 are even more compelling. We can point up to the binding site, but it’s also kind of clear that looking under the variable is a kind of let inlining operation, so the infinite expansion of the rational term is better motivated.

Semantically speaking, I’m not sure what this all means.

# python style knot tying of rational lambda
rat_lam = ["lam", ["lam", ["var", None]]]
rat_lam[1][1][1] = rat_lam
rat_lam

['lam', ['lam', ['var', [...]]]]

E = EGraph()
for i in range(2):
    rat_lam = E.makeset()
    rat_lam2 = E.makeset()
    varnode = E.makeset()
    E.observe(rat_lam, ("lam", (rat_lam2,)))
    E.observe(rat_lam2, ("lam", (varnode,)))
    E.observe(varnode, ("var", (rat_lam,)))
print("duplicate lambdas", E)
E.rebuild()
print("deduped lambdas", E)

duplicate lambdas EGraph(enodes={}, uf=[0, 1, 2, 3, 4, 5], obs={0: ('lam', (1,)), 1: ('lam', (2,)), 2: ('var', (0,)), 3: ('lam', (4,)), 4: ('lam', (5,)), 5: ('var', (3,))})
deduped lambdas EGraph(enodes={}, uf=[0, 1, 2, 0, 1, 2], obs={0: ('lam', (1,)), 1: ('lam', (2,)), 2: ('var', (0,))})

Bits and Bobbles

Question: How does once recognize egraphs that resulted from well founded term, union insertions?

A possible table of correspondences:

HashCons/Egraph Automata
node table observation table
f a -> a a -> f a
algebraic coalgebraic
hash cons minimize
rebuild minimize
least fixed point greatest fixed point
union find? partition refine
Congruence Closure Unification
Infer up infer down
Bottom Up Ematch Top Down Ematch

I wonder what the relationship of this post to https://www.ijcai.org/Proceedings/16/Papers/631.pdf codatatypes in cvc5 is.

The origins of these considerations come from trying to make sense of the tree automata ~ egraphs analogy. This topic had me seeking out automata theory and trying to reconcile how partition refinement could be monotonically added to egraphs. I don’t think the analogy to tree automata persay is involved in the above post. These works viewed the egraph/enode table itself as an automata, whereas I am injecting an automata-like thing obs to work alongside the enodes table in synchrony.

Should state ids (object ids OId) be a separate enetity from eclass id? We could

Primitives (primitive bool, i64, strings as seen in egglog) play better as observations than they do as lifted enodes. If an id is observed to be a primitive, that is a very canonical observation of that thing. Likewise for constructors. This is part of why I’m against the use of the keyword datatype in egglog for what are basically just functions. datatype and codatatype should imply useful injectivity, well foundedness / occurs check, or productivity conditions.

I’m not sure what a surface language should look like. Copatterns?

There is still the possibility of dangling makeset. If you makeset and then loose the reference to that, it’s a memory leak.

Resolving Observation collisions. There are different options. Co-merging of cofunctions.

  • Just fail if we have too distinct
  • Make observations eids and call union on collision
  • Unify by asserting arguments of observations be unioned
  • Just pick one of the two

From category stuff, we know algebraic things look like f a -> a and coalgebraic look like a -> f a whatever that really means.

The hash cons is a way of minimizing the construction of trees. I think it is more elegant looking than automata minimization, even though its kind of the same thing, because we are shallowing embedding inside of programming languages for which control kind of flows in a wlell founded way from the top of the file to the bottom. I don’t exactly know what a truly coalgebraic lamgiage would look like, but I’d guess that if such a thing makes sense, automata minimziation will be more elegant than hash consing.

Maybe something more like verilog? Erlang? Assembly?

Yihong has some russian paper where there were automatlike egraphs. How in the world am I going to find that?

The two implementations I have in mind for unification are a prolog style variables = refcell and a minikanren style substitution mapping. This co-egraph style separates the variable variable interactions into the union find and the variable-constructor interactions in the observation table. This is kind of a sensible spearation of concerns in my opinion. You could implement this is ref-cell style using a refcell that has a union find pointer to other variables and an lazy observation pointer to eventually be filled in by a functor. “Rebuilding” would then be looking up the union find tree to copy down any filled in observations.

mcrl2 and maude boith have a mixture of term rewritey and statey things they keep separate. This is another point in that design space

Supercompilation is egraph flavored. Maybe the states here can be used for this purpose.

Where does the occurs check come in?

https://dl.acm.org/doi/10.1145/3428195 contexts and “co-functional” dependencies in datalog for typechecking (edited) https://www.youtube.com/watch?v=1lL5KGVqMos&ab_channel=ACMSIGPLAN it has a video (edited)

Observations can have a notion of refinement. In the post, I only had two points in this lattice, observed and unexplored. But we can also have more ocmplex lattices for observations. For example, we can drop fields of the observations (in any order?), and that will presumably fuse more states as being equivalent. A bit fishy.

To make this stuff fast, smash together egg and boa. Talk to Max Willsey and Jules Jacobs. There probably needs to be more indices and more incrementality.

We have kind of made the egraph primary it feels like Is there a way to make the observations primary? Different ways of fixpointinf coq datatyes. Inductive foo a := ThisCase of a | MyCase of a. Coinductive MyRecord := { myfield : foo MyRecord }.

Notes

egrapgs modulo obersvations automata egraphs

What is the point of constructors?

  1. injectivuity let’s us know two things difenitely aren’t equal
  2. where does well foundedness come in? Detect unsoundness in our reasoning? Seems weak. Combined with context could be useful.
  3. In pattern matching? We could restirct to “well founded matches”? a = Cons(b,xs)

PEGs need to describe streams Streams are conductive things We can use automata minimization to determine two objects are the same.

cofunctions monotonicity requires obersvations go down. partition ids

Go through old insane egglog notes.

mcrl2 + egraphs. I think mcrls has term rewriting. Jules jacobs https://dl.acm.org/doi/abs/10.1145/3571245 new netkat. damien pous https://mcrl2.org/web/index.html Maybe use mcrl2 to prototype?

maude has a notion of transition system and object orientation does it do minimization

Machine states. Branching on unknowns, but then collecting back up?

Simple automata minimization

Could I do coegraph as a container?

data F = F F
f = F f

Landin’s knot

f = []
f.append(f)

An egraph of a single node is impossible to create via adding ground terms.

Use positive terms. If a pid isn’t in the coenode table yet, it is unexpanded. “Fully obseravable” not “unobserved”. Unexpanded not unobserved

If we tie break union find via min, then once something goes negative, there is something concretely observasble / distinguishable about it. Like we could have copatterns and an eqsat rule that encodes closure of an object. hd(x) = a, tl(x) = b -> object(x) = Cons(a,n)

Are the obersevations enodes? Maaaaaaybe. Also, I think it’d be nice to make final stuff observations. Like cons

The coniductive “record” isn’t identified with p, it is the observation of p

stuff in

Are two pids definitely not equal? No.

enodes : coenodes : final/constants : Dict[Cid, base values]

automatalog

closed and open worlds disequality

You can forget observations. You shouldn’t learn new observation though. That can split entities that have been merged, which is non-monotonic “No observation”

In coq, sometimes I’ve wanted a fixed point and there are different ways of factoring between condutctive and inductive definitions. This might be wat is happening here.

starting pid should be a partition of size 1 [x]?

duals - unification is dual to congreunce closure disjoint set is dual to union find

tantalizing but so far useless.

definition by recursive equations often leads to coinductive situatiosn x = a + bx read as x -> a + bx x_n+1 <- a + b x_n is an approximation process. but x -> a + b x is the solution zero = Cons(0, zero) coinductivwe equations

lambdas can be written as rational trees lam(var(X)) = X is lam x. x

T1 = lam(T2), T2 = lam(T3), T3 = var(T2) is \x y. y

Let bindings are more compelling let x = e1 in e2. Why bother? let(t, )

Huh. If I union two things that are observed, then I should traverse down their observations. e1 = e2 e1 = cons(a,b) e2 = cons(c,d) Then union(a,c), union(b,d)

Observations are assumed injective. c() = c -> a = b, c = d This is not congruence. Nor is it the contrapositive of congruence. Unification is coalgerbaic. Or something.

nil = cons() just abort.

multipattern hd(?x) = a, tl(?x) = b -> observe x = cons(a,b)

So could I make a prolog with these semantics? A minikanren. Can we do this with triangular substutitions purely functionally? X = cons(A,B) is a coequation.

cons(A,) = is an egraph equation.

Is this sufficient for clp set?

bottom up ematching is natural for enodes, top down is natural for observations

Literals don’t need wrappers (?) Literals are an observation. two literals being equal is insocnsitent. But fact(2) = 2 isn’t

unification modulo egraphs

clpset EW45

yeah, its interesting. This decoupling of the var -> var case and the constructopr -> var case was a thing that I mentioned in my GRS summary. It is also a distinction that is maybe kind of nice for unification. Flex-flex, rigid-rigid, rigid-flex = union, merge_obs, observe These are the subvases of a typical unification algorithm

The var -> flatterm observation could be seen as a simplified canonical representation of the substitution mapping coming out of the unification. It could also be thought of as the refcell character of the unification.

Does the coegraph support unification variables? Are the “vars” in egraph always unification vars?

What happens if I use the gauss or grobner union find? Do I get E-unification?

There is a non-det choice of ways to resolve a unification clash. All the things in the enodes table with that constructor. Or we could just freeze the clashes and save them? self.clashes = []. To be reconciled later. We could also assert dif/2 constraints. And maybe those are disallowed clashes. Or mark irreoncilable constrcutors. This is a bit like turning uniification into a constraint store. Attributed variables. Some variables are attributed by eclasses. We could resolve irreconcilable clashes by inserting them into the enode table? And then just picking one or having the observation being the id of the observation class.

https://www.cs.bu.edu/fac/snyder/publications/UnifChapter.pdf

The idea that observations are rigid hurts a bit. Do I reflect observations into the enodes table also? Or vice versa, some special enodes are considered observational / definitional / datatype constructors and auto reflect into observations. This could be represented by rules. injectivity was one of the original egglog0 examples and yihong wanted to do e-unification. Rules can’t achieve the automata minimization thing / rational term interning. Also yihong wanted hinldey milner

coegraphs: e-unification, streams, pegs

if x = y + z, what happens. That is a unify(x, y+z)

Unification is made even lazier. That’s kind of interesting. The recursion is pushed to rebuild. This is like how egg made congruence closure lazy. The classic pointery CC/egraph has to eagerly canonize. This can be done in the pointer refcell unification if they hold two fields, the variable uf field and an observation field. struct Var = {uf : Var, obs: Obs} The var tree could be seen as unification alternatives? Kind of like the aegraph union nodes. Maybe this is a way of holding all unifiers as a set? That’s intriguing. The sharing action of the egraph but across unifiers. But to collapse this, we would want to pick a consistent set of which unifier (best in some objective sense, not best as in most general). Is this the extraction problem? Lazy E-unification

If I combine gauss + x = f(x,..) rational terms, can i describe infinite series?

Extraction becomes trivial. Is there some dual operation that requires search now (add_term)? Or can be optimized? Find the best variable for some observation?

goal : Callable[CoEgraph, list[CoEgraph]]

class CoEgraph():
    def __init__(self):
        self.enodes = {}
        self.obs = {}
        self.uf = []
    def find(self, x):
        while self.uf[x] != x:
            x = self.uf[x]
        return x
    def makeset(self, x):
        y = len(self.uf)
        self.uf.append(y)
        return y
    def union(self, x, y):
        x = self.find(x)
        y = self.find(y)
        self.uf[x] = y
    def add_term(self, t):
        pass
    def rebuild(self):
        newenodes = {}
        for (head, args), eid in self.enodes.items():
            newenodes[(head, tuple(self.find(a) for a in args))] = self.find(eid)
            # congruence
        for eid, (head, args) in self.obs.items():
            self.union(eid, newenodes[(head, tuple(self.find(a) for a in args))])

            

eqs : dict[setid, set(urelement | setid)]
# compress via completion
# This is for finite sets. The set in the observations is all elements of the set.
# the analog of the occurs check
# If we tack on a union find for the urelements, we get a monotonic clp(set)
# This is probably implementatble as a CHR
# Is this in the setlog literature? They are obviously aware of non well founded sets.
# setids are _not_ unification variables.
# in the presence of disequality, things can be inconsistent / failure
# unification of sets is unification of their set structures. With non ground urelements, this is the otught bit. If they are ground, it's fine (?).