Bouncing a Ball with Mixed Integer Programming
Edit: A new version.
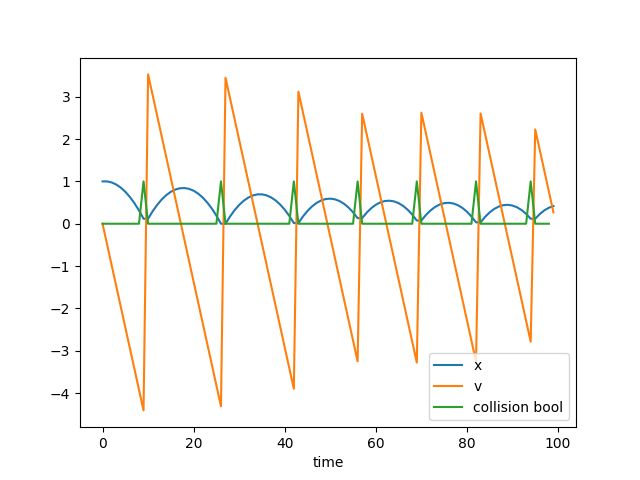
Here I made a bouncing ball using mixed integer programming in cvxpy. Currently we are just simulating the bouncing ball internal to a mixed integer program. We could turn this into a control program by making the constraint that you have to shoot a ball through a hoop and have it figure out the appropriate initial shooting velocity.
import numpy as np
import cvxpy as cvx
import matplotlib.pyplot as plt
N = 100
dt = 0.05
x = cvx.Variable(N)
v = cvx.Variable(N)
collision = cvx.Variable(N-1,boolean=True)
constraints = []
M = 20 # Big M trick
#initial conditions
constraints += [x[0] == 1, v[0] == 0]
for t in range(N-1):
predictedpos = x[t] + v[t] * dt
col = collision[t]
notcol = 1 - collision[t]
constraints += [ -M * col <= predictedpos , predictedpos <= M * notcol]
#enforce regular dynamics if col == 0
constraints += [ - M * col <= x[t+1] - predictedpos, x[t+1] - predictedpos <= M * col ]
constraints += [ - M * col <= v[t+1] - v[t] + 9.8*dt, v[t+1] - v[t] + 9.8*dt <= M * col ]
# reverse velcotiy, keep position the same if would collide with x = 0
constraints += [ - M * notcol <= x[t+1] - x[t], x[t+1] - x[t] <= M * notcol ]
constraints += [ - M * notcol <= v[t+1] + 0.8*v[t], v[t+1] + 0.8*v[t] <= M * notcol ] #0.8 restitution coefficient
objective = cvx.Maximize(1)
prob = cvx.Problem(objective, constraints)
res = prob.solve(solver=cvx.GLPK_MI, verbose=True)
print(x.value)
print(v.value)
plt.plot(x.value, label='x')
plt.plot(v.value, label= 'v')
plt.plot(collision.value, label = 'collision bool')
plt.legend()
plt.xlabel('time')
plt.show()
Pretty cool.
The trick I used this time is to make boolean indicator variables for whether a collision will happen or not. The big M trick is then used to actually make the variable reflect whether the predicted position will be outside the wall at x=0. If it isn’t, it uses regular gravity dynamics. If it will, it uses velocity reversing bounce dynamics
Just gonna dump this draft out there since I’ve moved on (I’ll edit this if I come back to it). You can embed collisions in mixed integer programming. I did it below using a strong acceleration force that turns on when you enter the floor. What this corresponds to is a piecewise linear potential barrier.
Such a formulation might be interesting for the trajectory optimization of shooting a hoop, playing Pachinko, Beer Pong, or Pinball.
using JuMP
using Cbc
using Plots
N = 50
T = 5
dt = T/N
m = Model(solver=CbcSolver())
@variable(m, x[1:N]) # , Bin
@variable(m, v[1:N]) # , Bin
@variable(m, f[1:N-1])
@variable(m, a[1:N-1], Bin) # , Bin
@constraint(m, x[1] == 1)
@constraint(m, v[1] == 0)
M = 10
for t in 1:N-1
@constraint(m, x[t+1] == x[t] + dt*v[t])
@constraint(m, v[t+1] == v[t] + dt*(10*(1-a[t])-1))
#@constraint(m, v[t+1] == v[t] + dt*(10*f[t]-1))
@constraint(m, M * a[t] >= x[t+1]) #if on the next step projects into the earth
@constraint(m, M * (1-a[t]) >= -x[t+1])
#@constraint(m, f[t] <= M*(1-a[t])) # we allow a bouncing force
end
k = 10
# @constraint(m, f .>= 0)
# @constraint(m, f .>= - k * x[2:N])
# @constraint(m, x[:] .>= 0)
E = 1 #sum(f) # 1 #sum(x) #sum(f) # + 10*sum(x) # sum(a)
@objective(m, Min, E)
solve(m)
println(x)
println(getvalue(x))
plotly()
plot(getvalue(x))
#plot(getvalue(a))
gui()
More things to consider:
Is this method trash? Yes. You can actually embed the mirror law of collisions directly without needing to using a funky barrier potential.
You can extend this to ball trapped in polygon, or a ball that is restricted from entering obstacle polygons. Check out the IRIS project - break up region into convex regions
https://github.com/rdeits/ConditionalJuMP.jl Gives good support for embedding conditional variables.
https://github.com/joehuchette/PiecewiseLinearOpt.jl On a related note, gives a good way of defining piecewise linear functions using Mixed Integer programming.
Pajarito is another interesting Julia project. A mixed integer convex programming solver.
Russ Tedrake papers - http://groups.csail.mit.edu/locomotion/pubs.shtml
https://www.youtube.com/watch?v=gJBitAHDPsA
Break up obstacle objects into delauney triangulated things.
www.mit.edu/~jvielma/presentations/MINLPREPSOLJUL_NORTHE18.pdf