That proofs are things (mathematical objects) is a cool meta awareness that is one of the payoffs of studying mathematical logic.

The Curry Howard correspondence https://en.wikipedia.org/wiki/Curry%E2%80%93Howard_correspondence has produced an awareness in the right circles of the programming or CS world that simply typed lambda terms are proofs objects of natural deduction for propositional intuitionistic logic or that that dependently typed terms are proofs objects of a more complex logic. For example lam x : A. x is a proof object of the proposition A -> A. These are not the only proof objects in the world, nor the simplest ones IMO and not all reasonable ways to think about proofs fit in the Curry Howard paradigm. Curry Howard does not own the concept of proof even if the system is flexible and a nice design principle. Turn off your dependent typed brain if you have one or you will miss the intent with which I write this.

Some of my favorite examples of proof objects are

Paths are Proof Objects of Connectedness in a Graph

For small graphs, connectedness does not seemingly require proof, since it is a topic in algorithms class on how to efficiently compute connectivity in polynomial time. Even in this case, it is easier to check a path than to find it.

However if you consider big big graphs, it can be impossible to completely examine all the edges.

A equational reasoning system can be modelled as a giant graph of terms with an edge between each term that can be rewritten by applying an equation. The vertices of this graph are all the terms. We can produce a computable edge predicate Term -> Term -> Bool or Term -> [Term] that tells us all the axiom equations that may apply to a particular node, but

Proof producing union finds are a way the make a spanning tree through a graph. https://www.cs.upc.edu/~roberto/papers/rta05.pdf https://en.wikipedia.org/wiki/Kruskal%27s_algorithm https://arxiv.org/pdf/2504.10246

The two divisor is a witness of evenness

If you give me the number that I need to multiply by 2 to get x, that is a bit easier in my mind than figuring out how to divide a number by two. According the the BHK interpretation https://en.wikipedia.org/wiki/Brouwer%E2%80%93Heyting%E2%80%93Kolmogorov_interpretation , we should associate witness information like this with existential statements like even(x) := exists y, 2*y = x . The BHK interpretation is the thing that the Curry Howard correspondence bakes in so thoroughly it is hard to understand the general concept.

Proofs of linear equations

We can add together linear equations like 3x + 4y = 7 and -x + 70y = 2 to get new equations 214y = 13. We learn this in school as part of a method of Gaussian elimination.

What this means is that a possible proof object is a vector over the basis of equation axioms. If we can combine the axioms equations %E$ to get some goal equations $G$ like $a_1 E_1 + a_2 E_2 + … = a^T \cdot E = G$ then the vector $\vec{a}$ is a proof object. I dare you to tell me that a vector is not a valid mathematical object. Some of these equations can be redundant which induces a quotient on the vector space of linear equational proofs.

Proofs of linear Inequations

In linear programming, dual vectors are proof objects / certificates of optimality.

You again can linearly combine inequalities only using positive coefficients. A negative number flips the direction of the inequality -2 * (42 >= 4) ---> -84 <= -8. An optimal dual vector l^T combines the linear inequalities to get the cost vector c on one side and the cost of the found primal solutionV on the other l^T (A x <= b) ---> c^T x <= V.

You do not need to see how the dual vector was found in order to check it.

https://en.wikipedia.org/wiki/Dual_linear_program

See section 5.5 https://web.stanford.edu/~boyd/cvxbook/bv_cvxbook.pdf Although I remember the course being clearer on the point about the dual being a certificate.

Polynomial combinations of polynomials

Similarly to the two above if you want to show that p(x,y,z) is zero under the assumption q1, q2, q3,... = 0, a polynomial combination of them does show this (although it isn’t a complete proof procedure depending on what you want. I can’t derive (x - 2) from (x -2)**2. Really these are proof objects that p is in the ideal https://en.wikipedia.org/wiki/Ideal_(ring_theory) generated by the q). This is a vector of polynomials. These polynomials themselves may be redundant like how linear equations were redundant. These redundancies are called syzygies https://en.wikipedia.org/wiki/Linear_relation

A Bool is a proof object

If I say that a correct automated theorem proving procedure found a proof, then just saying that is a proof object at the extreme. All proofs require varying degrees of reconstruction. We usually erase all sorts of little things that are easily reconstructed on the other side. Once I know that the theorem is proven, I can just run the ATP again the reconstruct the proof.

First order theorem provers are solving a semidecidable problem. A different slightly better proof object than a bool is the number of steps / “gas” the program has to run to find it’s solution.

Traces are Proof objects

Many many proof objects are traces of theorem proving systems. If you believe you somehow built a theorem prover, the substeps of this theorem prover that led to a success are proof objects. You could record every assembly instruction ran, but usually it’s nicer to log just some higher level summary steps.

This is a viewpoint useful for SAT solvers, MIP solvers, datalog provenance, etc. It’s a really useful principle to understand what a proof object might even look like coming out of these systems. Just print / log every time you do something interesting!

UNSAT certificates basically traces of useful learned clauses in a SAT solver. The learned clauses are combinations of previous clauses using resolution. https://www.cs.utexas.edu/~marijn/drat-trim/

Datalog/prolog provenance basically carries an extra tracing parameter in every predicate. Traces of a prolog solve are proof objects. https://www.philipzucker.com/metamath-datalog-provenenance/ . Even just a timestamp is a useful proof object since it tells us where to look to reconstruct. https://www.philipzucker.com/snakelog-post/#Timestamps%20and%20Provenance

One (too) cute way to carry proof parameters is in DCGs in prolog. The easiest way to trace isn’t to turn on some wacky built-in, it’s to just thread a log list through your computation that you append to.

prove(A > A)       --> [id].
prove(A /\ _ > A)  --> [fst].
prove(_ /\ B > B)  --> [snd].
prove(A > A \/ _)  --> [inj1].
prove(B > _ \/ B)  --> [inj2].
prove(false > _)   --> [initial].
prove( _ > true)   --> [terminal].
prove(A > B /\ C)  --> [pair], prove(A > B),  prove(A > C).
prove(A \/ B > C)  --> [case], prove(A > C),  prove(B > C).
prove(A > C)       --> [comp], prove(A > B),  prove(B > C).

MIP certificates are a tree of dual vectors (assuming branch and cut).

https://cs.paperswithcode.com/paper/verifying-milp-certificates-with-smt-solvers VIPR certificates https://arxiv.org/abs/2312.10420 Satisfiability modulo theories for verifying MILP certificates

https://github.com/ambros-gleixner/VIPR so SCIP can output this stuff? Huh.

https://github.com/ambros-gleixner/MIPcc23 mip reoptimization

Rewrite Proofs

Rewrite proofs have a couple different formats. See also what egg outputs https://docs.rs/egg/latest/egg/tutorials/_03_explanations/index.html .

A sequence of terms with position (how to get to subterm applied at) and eqaation used information tagged in between each
Congruence style. A cong node that takes in subproofs of all children equations and lifts them. Since rewrite proofs have a categorical flavor (has id and can be composed) the cong nodes have the flavor of a monoidal product functor (you can push compose above or below cong nodes. cong_f(p1) . cong_f(p2) = cong_f(p1 . p2) ). This gives some algebra of proofs. One can ask how to normalize proofs (See Terese). Congruence is the fancier version of grade school’s “do the same thing to both sides of an equation”. The first style is a flattening of this style.

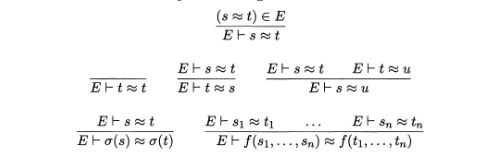
Sequent and Natural Deduction proofs

They are for serious trees you can write down in a programming language. It is important to not be confused about the different between the judgement the proof is for and the proof itself. These are kind of easy to get confused for some reason. The judgement is a tuple or set of formulas or something. The proof is this massive recursive tree with judgements at every node. You don’t have to use lambda calculus verbiage. Sequent calculus has proof terms in the curry howard style in the lambda mu mubar calculus https://en.wikipedia.org/wiki/Lambda-mu_calculus

Operations like Cut-elimination, negation normal form, cnf, dnf are for serious algoritms for transforming or using these proof tree data structures

UNSAT cores and Relevancy Pruning

A lighter weight proof object is an unsat cores, which at least prune for relevancy.

Maybe somewhat similarly, giving me the groundings of the rewrite rules used or datalog rules used is a huge help.

Good Rewrite Rules

A good rewrite rule system is a compressed proof object if you can guarantee I can run it and it will work. Each rewrite rule needs to be dignified from the axiom equations. Knuth bendix produces systems like this. But you can also produce rewrite systems specialized to a particular goal equation.

Numbered Lists

Hilbert style number lists of statements. If you refer to previous ones by number (or name). This is a bit what knuckledragger and metamath proof objects feel like

Bits and Bobbles

Hello from Paris!

I’ve had this one knocking around a while. You can see notes below that I think it would be good to actually program up all these proof objects.

A whole other branch down the proof tree is crypto proofs and certificates https://en.wikipedia.org/wiki/Zero-knowledge_proof https://en.wikipedia.org/wiki/Proof_of_knowledge https://en.wikipedia.org/wiki/Digital_signature Not entirely unrelated. If you have a trusted proof kernel, it can crypto sign it’s proof objects as validated in an LCF style.
The program text that produces proofs (tactics) is also proof objects. Complex ones.
https://en.wikipedia.org/wiki/Van_Kampen_diagram Van Kampen Diagrams are a visual proof object for the word problem of finitely presented groups.
https://en.wikipedia.org/wiki/Method_of_analytic_tableaux The graphs of tableau are proof objects. I could make a networkx graph or whatever and a check routine. Paths in connection matrices, although I haven’t grokked this one.
The stuff output by provers like vampire etc are kind of like traces. Little clues.
A SAT solution of LP feasibility are proof objects of the satisfiability of those problems.
NP doesn’t mean hard. What it means is that there is a certificate to the problem that can be checked in polynomial time. So all these problems have witnesses / proofs objects. They usually have the flavor of a constraint solution or SAT solution.
Ron Garcia pointed out this https://cacm.acm.org/research/program-correctness-through-self-certification/ Outputting the permutation of a sorting algorithm is a good one. Verifying that is slightly easier than redoing the sort. DWARF I think is an interesting target for a bisimulation proof object https://www.philipzucker.com/dwarf-patching/ as it already specifies a connection between high and low code for debugging purposes.
A similar thing is in parse don’t validate. https://lexi-lambda.github.io/blog/2019/11/05/parse-don-t-validate/ A parse tree is a proof object that a string is in a language. You can make a parse tree as a kind of trace of the parser. A related thing I like is to intrinsically sorted list Option (Int, [Nat]) which stores a starting point but then only differences. The Nat makes a drecreasing difference unprepresentable.
https://en.wikipedia.org/wiki/Proof_theory Proof theory is the study of proofs as mathematical objects. It has a focus on logicy stuff, sequent calc, natural deduction etc.
Sum of squares https://en.wikipedia.org/wiki/Sum-of-squares_optimization form of polynomials shows they are everywhere position. $p(x) = \sum b_n x^n = \sum a_i q_i(x)**2$$. You can parametrize this as $ p(x) = \vec{x}^T A \vec{x}$ with positive semidefinite $A$ https://en.wikipedia.org/wiki/Semidefinite_programming and go polymomoial by polynimial to linearly relate $a_i$ and $b_i$ coefficients. It is surprisingly a convex optimization problem.
I’ve never really understand the industry of SMT proof objects, but it’s out there.

https://microsoft.github.io/z3guide/programming/Proof%20Logs/ https://github.com/Z3Prover/z3/discussions/4881 https://cvc5.github.io/docs/cvc5-1.0.0/proofs/proofs.html Alethe LFSC Z3 had a light DRAT-like congruence format. What happened to that one?

What is your cutoff of Proof vs Not? Is Bool a proof object? Do proofs need to reduce from undecidable to undecidable? Do they need to reduce complexity?

https://en.wikipedia.org/wiki/Proof_complexity

Decidability vs undecidable. If we take decidability of theorems as meaning they don’t need proof, then we ignore sat certificates all sorts of stuff Complexity arguments. https://en.wikipedia.org/wiki/Proof_complexity#Proofs_of_polynomial_size_and_the_NP_versus_coNP_problem Probably there is no polnoymiasl bounded positional system.

But how do you defend against garbage with no relevant information context as a proof object?

automatable proofs https://knowledge.uchicago.edu/record/12840?ln=en&v=pdf https://www.youtube.com/watch?v=gIsNV-o3MgY&ab_channel=SimonsInstitute a sruvey of automatilbity. algorithm that given taut outputs an proof in a time polynomial in the length of the shortest proof available https://www.youtube.com/watch?v=SZ6TWaNt5LQ&ab_channel=SimonsInstitute

I have had debates with Graham and others about what should count as a proof object.

Proofs are actions or things that convince someone about the truth of something.

Paths in infinite graphs, even functional a path seems less straightforward. Indeed all proof search (in the sense of seeking an eumerable finite chceckable object) can be encoded in a graph search with richer vertices. It’s reachability kind of.

Vertices are sets of proven formula is one version. Kripke model of intuiotnsitc logic. But why?

type Graph = V -> V -> bool

type Graph = Stream (V,V)

There is such a strng proof calculus that it normalizes. Could also have Tree like nor Which proofs are the “same”

class Proof(): ...
class AddEq(): ...
class MulEq(): ...

# could eveb make MulEq as synpy Expr
#class MulEq(Add)

from sympy import *

x,y = symbols('x y')

Eq(3*x + 8*x, 34)

class LinProof():
    pf : list[tuple[float, Equality]] # or dict[Equality, Real]
    fm : Equality
    def __add__(self, other):
        if isinstance(other, LinProof):
            return LinProof(self.pf + other.pf, Eq(self.fm.lhs + other.fm.lhs, self.fm.rhs + other.fm.rhs))
    def __mul__(self, other):


def flatten(pf: Proof) -> LinProof:

Ineqaulity proofs Polynomial proofs

p1,p2,p3

- p

multiplation is kind of an or.

(x - 2)(x - 4)

- x - 2, x - 4

class RewriteStep():
    position : list[int]
    rule :
    vs :  
    t1 : 
    t2 : 

RewriteProof = list[RewriteStep]


class RewriteProof2():



class Cong():
    f : Function

class Conf():
    f : smt.FuncDeclRef

class 
class Trans():
    a: V ; b : V;  pf: PathProof

# like drat
class ResProof():
    pfpos : 
    lit : 
    clause : frozenset[smt.BoolRef]

#@dataclass(immutable=True)
class Sequent():
    hyps : frozenset[smt.BoolRef]
    concs : frozenset[smt.BoolRef]
class Proof():
    seq: Sequent
    fm: smt.BoolRef
class Proof1(Proof):
    pf : Proof
class Proof2(Proof):
    pfA : Proof
    pfB : Proof
class Rand(Proof2): ...
class RAnd(Proof2): ...

class RAnd(): pfA : Proof; pfB; Proof; fm : smt.BoolRef; seq : Sequent
class ROr(): pfA : Proof; fm : smt.BoolRef; seq : Sequent
class LOr(): pfA : Proof; pfB : Proof; fm : smt.BoolRef; seq : Sequent

def check(Proof):
    match pf:
        case RAnd(pfA, pfB, fm, seq):
            assert fm == And(pfA.fm, pfB.fm)
            assert pfA.seq == pfB.seq
            assert pfA.seq.hyps == pfB.seq.hyps
            assert pfA.seq.concs == pfB.seq.concs
            assert pfA.seq.hyps == seq.hyps
            assert pfA.seq.concs == seq.concs
        case ROr(pfA, fm, seq):
            assert fm == Or(pfA.fm)
            assert pfA.seq == seq
        case RImplies():
        case RNot()



# atctic
def rand(fm, seq): -> tuple[tuple[Sequent, Sequent], Callable[tuple[Proof, Proof, Proof]]]
def ror(): ...

# tactic. It's a lens.
def nnf(fm): ...
def cnf(fm) -> tuple[Sequent, Callable[Proof, Proof]: ...




def resolve(seq : Sequent) -> Proof: ...


def cut_elim(): ...

class NDJudge():
    ctx : list[smt.BoolRef]
    fm : smt.BoolRef
class NDProof():
    judge : NDJudge
class AndIntro(NDProof): pfA : NDProof; pfB : NDProof
class AndElim1(NDProof): pfAB : NDProof
class AndElim2(NDProof): pfAB : NDProof
class OrIntro1(NDProof): pfA : NDProof
class OrIntro2(NDProof): pfB : NDProof
class Weaken():
class Var(NDProof):

def check(pf: NDProof):
    

The lambda mu style proof terms. Translation to and from ND If we used smt.Sort as formula objects could use z3 lambdas as proof terms.

class HilbProof(): ...
class Modus(HilbProof):
    ab : HilbProof
    a : HilbProof
    fm : smt.BoolRef

def check(HilbProof):

proof transformations

There are a number of transformations in logic and automated reasoning that are described as transformations on formulas that carry along semanticsa somehow (equisastifiability). The issue with this from my perspective is that this semantics is somewhat ethereal if you are inside a programming language. You don’t really have a great way of talking about abstract infinite sets.

Almost every introduction to logic starts with propositional truth tables.

This comes about somewhat because what proof objects even are is vague. Once we have a concrete notion of proof object.

negation normal form, disjunctive normal form, conjubctive normal form, skolemization, cut elimination

subformula property

natural -> hilbert is analgous to compiling to combinators natural <-> sequent

https://www.cs.cmu.edu/~fp/courses/atp/schedule.html

from typing import NamedTuple, Optional
class Proof(NamedTuple): judge: object; subproofs: list["Proof"]
class Proof(NamedTuple): rule: str; thm
class Proof(NamedTuple): data: object; subproofs: list["Proof"]
# We can do a style where we have one constructor per proof rule, or a style of a generic Proof object
# Thisi s very analous to trhe situation in terms with a Fn(str,args) version vs a one constructor per fn symbol

Proofs are traces

Big principle. Proofs are traces.

There are many proof methods. There are many traces and hence many proof formats.

truth tables

Are truth tables proof objects? They kind of suck. They are so huge that it is much worse to process the table than to regenerate it.

A propositional formula is decidable, so by some standards doesn’t nmeed proof objects? Thats silly though.

It offers no complexity improvement to have the certificate. May as well have the certificate be junk or not exist

They also have semantic smell.

A proof object of

forall M, (M

= A)

This proof object is a tree (a list) of all the rows. n	= A is a metalogical side condition.
`all _ < _ \|= _` `all M \|= A` are two different judgements.

all M < n |= A   n |= A
-----------------------
   all M < n+1 |= A  


   all M < n |= A    2**maxvar(A) = n 
--------------------------
       all M |= A

truth tables for non classical logics. Kripke: enumerate number of worlds. generate all accessibility relations. Derive some bound from the formula. That’s the confusing part. Probably some kind of modal depth.

Rewrite proofs

rewrite proofs. rw(t, rule) = s

cnf(r1, axiom, rw(f(f(X)), r1) = X). cnf(r1, axiom, ~(rw(T, R) = T1) | rw(f(T), cong(R)) = f(T1)).

% relational form cnf(r1,axiom, eq(f(f(X)), X, r1)).

tff( , type, pf : $tType) tff( type, syn : $tType) tff( type, sem : $tType) tff( type, start : pf > syn) % dom (end : pf > syn) % cod tff eval : syn > sem) tff( reflect : sem > syn) tff( type, end : pf > )

tff( canon, syn > syn ) canon(T) = reflect(eval(T))

refl : syn > pf symm : pf > pf comp : pf * pf > pf congf

direct conversion of proof stustures seems more conceptually straightrforward to me than some hand waving about herbrand interpretations.

https://dl.acm.org/doi/10.1145/174652.174655 Equational inference, canonical proofs, and proof orderings

rewrite proofs are a sequence of (position, axiom) tuples interspersed with terms. On the edges and vertices. [([0,1,0] ,r1), ([0,1], r2), ([0], r3)]

Redundancies. Some rewrites can be reordered. So a sequence is perhaps silly. The cong rules let you factor into the independent parts. Kind of a “par” parallel rule.

More implicit is to erase the position. Or erase the rule and position and just list a sequence of terms. “equality with transtivity is decidable” add it to the conversion rules.

Any rewrite system that works for the particular question is a proof. It is a compact way with a little bit of algorotihmic content. You could pick a particular imperative strategy even if not confluent on your starting point. The completed rewrite system is a proof for all pairs. Or it can just be a big step subroutine. (normlize into cnf, then yada yada). Compaction and big step proof discovery via anti unification?

Is the knuth bendix rule kind of like extensionality.

Or its a proof tree, which kind of refactors this data congf(refl, r1) : f(a, b) = f(a, c)

reminsecent of matrix korncker rules. Fusion rules. Monoidal categoiry rules. comp(congf(A,B) , congf(C,D)) = congf(comp(A,C), comp(B,D)) comp(symm(R), R) = refl comp((comp(F,G)), H) = comp(F, comp(G,H)) symm(symm(R)) = R symm(refl(T)) = refl(T) symm(congf(A,B)) = congf(symm(A),symm(B))

symm is like inverse matrix.

univalence? (comp(f,g) = refl(T)) & comp(g,f) = refl(T1) <-> f = g term1(comp(f,g)) = term1(refl(T)) <-> f = g T1 = T2 as terms?

I’m seeking a way to turn only some proofs into intensional proofs. This is maybe related to quotienting out in sequence. Or having systems of E baked in. Is E-modulo and the homotopy thing related? Their quest is also about baking in. Huh. baking in casting. Baking in isomorphisms

exists([F,G], forall(T, term1(comp(F,G)) = T))

proof irrelevance. term1(P) = term1(Q) & term2(P) = term2(Q) <-> P = Q

extensionality. But this makes the terms equal? exists(P, term1(P) = T1, term2(P) = T2) <-> T1 = T2

ismorphism in the model?

simplical sets?

Yes, this is like A

- B as a category. comp, id

These cong combinators are indexed krons. That reminds me of anyons.

call it refl or id. It should be indexed by the term it is being applied at. comp(refl(T), F) = F. This is problematic for the usual reasons. T actually has to be the term. terms are like objects?

Hmm. Could I revisit using eprover? https://www.philipzucker.com/theorem-proving-for-catlab-2-lets-try-z3-this-time-nope/ There was this idea of using knuckeldragger to show its ok to delete junk in my axioms.

an indexed version of otimes. congf = \otimes_f

proof orders says

The proof tree can be flattened in different ways.

traces of proving processes are proof objects. We are making trace data structures of the proving process. Subtrees kind of factor, which is the mariaculous character of terms.

https://link.springer.com/chapter/10.1007/3-540-18508-9_23 Foundations of equational deduction: A categorical treatment of equational proofs and unification algorithms

https://www.mi.fu-berlin.de/inf/groups/ag-ki/publications/free-logic/article-20.pdf Automating Free Logic in HOL, with an Experimental Application in Category Theory

What does egg output. Egglog. Eprover twee jbob / nqthm maude? z3 proof objects. cvc5

syzygies s polynomials S(g1,g2) = sum an * gn

There is a rewrite proof connecting all critical pairs. Sure.

a*gi = 0 is syzygies. p[.. s] = q[… t] is set of term equations

New generating constants? a,b,c, f() –> p,q,g(X)

idea: sorted lists can be converted into instrinsically sorted lists by considering differences.

Using my string rewriting thing when z3 knuith bendix might be interesting. Kind of reminscient of K’s store thing. contexts

In a curious way, I guess the quest in DTT is also about equations modulo. But like equations modulo isomorphisms or equations modulo casting

permutation equivalence. standardization https://www.ti.inf.uni-due.de/publications/bruggink/thesis.pdf Terese chapter 8

rewriting logic

mellies

https://ncatlab.org/nlab/show/Tietze+transformation#tietzes_theorem https://en.wikipedia.org/wiki/Group_isomorphism_problem https://docs.gap-system.org/doc/ref/chap48.html#X782985197BE809BF I don’t know what the lesson here is

https://en.wikipedia.org/wiki/Module_homomorphism isomorphisms of rings?

https://en.wikipedia.org/wiki/Nielsen_transformation

Combinatorial group theory https://projecteuclid.org/journalArticle/Download?urlid=bams%2F1183548590 the word problem and the isomorphism problem for groups … stillwell

cancellative semigroups rather than groups is sufficient for egraph?

ground proof theory is possibly ok too? Maybe any good groundness, linear, grobner, multiset etc proof theory is also good?

https://docs.rs/egg/latest/egg/struct.Explanation.html

(+ 1 (- a (* (- 2 1) a)))
(+ 1 (- a (* (Rewrite=> constant_fold 1) a)))
(+ 1 (- a (Rewrite=> comm-mul (* a 1))))
(+ 1 (- a (Rewrite<= mul-one a)))
(+ 1 (Rewrite=> cancel-sub 0))
(Rewrite=> constant_fold 1)

Interesting. rw(t, rule) form rw(t, id) = t rw(rw(t), r1), r2)

(+ 1 (- a (* (- 2 1) a)))
(+
   1
   (Explanation
     (- a (* (- 2 1) a))
     (-
       a
       (Explanation
         (* (- 2 1) a)
         (* (Explanation (- 2 1) (Rewrite=> constant_fold 1)) a)
         (Rewrite=> comm-mul (* a 1))
         (Rewrite<= mul-one a)))
     (Rewrite=> cancel-sub 0)))
(Rewrite=> constant_fold 1)

eq(t1,t2,r) = canon(t1) = canon(t2)

homo(H) = ( H(f(X.Y)) = f(H(X), H(Y)) & …) H @ (f @ Y) = f @ (H @ Y) iso(G,H) = H @ G @ X = X & G @ H @ Y = Y could this enumerate?

graph isomorphism

succ(X) <=> b1(b0(X)) double1(succ(X)) = succ(succ(double1(X)))

zero = zero b1(X) = succ(double(X)) b0(X) = double(X)

succ(zero) = bsucc(bzero) = b1(bzero)

carry(bzero) = b1(bzero) carry()

succ(b0(X))

iso(iso(F,G), eq(X,Y,p) Can I even confirm this is an iso via eprover?

We could prefer b0,b1 over succ for sure. Is the point a john major like equality where you can transfer over and come back?

If I did want to have group isomorphism lifted to =. To show that my triangulted thing = the canonical form of the group

Proof objects are sometimes internally storeed in the same ast data structures. Because why implement another thing? This is the same moitvation of mathemticians. Why have a theory for two things if they can be unified

Geometric group theory. van kampen diagrmax

dehn functions - bound size of van kamep nfiagram

term metrics https://www.itu.dk/~paba/pubs/files/bahr11rta-slides%20(handout).pdf

https://link.springer.com/chapter/10.1007/978-3-031-63501-4_20 solving quantitative equations. hmmm. Useful for taylor O(x^n) equal or epsilon error equal? “Context” ? https://link.springer.com/chapter/10.1007/978-3-031-63501-4_20 Elements of Quantitative Rewriting Plotkin quantiative equational https://www.cambridge.org/core/books/foundations-of-probabilistic-programming/quantitative-equational-reasoning/4B76BCCD4D6A3A37459C35ED2CE5FF93 mkarov decision precorsses equational https://www.cambridge.org/core/books/foundations-of-probabilistic-programming/819623B1B5B33836476618AC0621F0EE

old 07/24

What is a proof?

I think a lot of clarity is gained by examining a couple of cases where there is a reasonable notion of proof

There is a mushy boundary between things requiring proof

paths in a graph are proof of connectivity. Silly right? Computing a path is so easy. Algos 101. Well, if the graph is exponentially large or infinite, not so clear.
Satisfying assignments.
Dual vectors. For linear equations can show unsolvability. For inequalities can show minimality or unsolvability. For polynomial systems, can show unsolvability. This is Nullstullensatz (?) https://en.wikipedia.org/wiki/Hilbert%27s_Nullstellensatz https://terrytao.wordpress.com/2007/11/26/hilberts-nullstellensatz/
UNSAT certificates. Traces / Transcripts
Trees

Termination certificates.

Proof normalization - Why? Cut elimination - why? It’s a way of leaving

There is some machine phi(x,p). Computing phi(x,p) given p is presumably easier than guessing p. Perhaps phi may be poly time, or at terminating. If given p, phi is possibly still nonterminating, that is saying proof checking is undecidable, something that comes up in extensional type theory for example.

if phi(x,_) is N^3 and phi(x,p) is N, is that not a proof object?

mip proofs

NotMin is a SAT-like NP problem. Give me a better solution and that certifies that mine is NOTMIN

MIN is an UNSAT-like co-NP problem. Somehow show me there is no better solution.

So minimization of producing is something akin to the intersection of NP and co-NP

Linear programming is beautiful because of the duality principle, where te dual vector is a proof certificate deomsntrating the minimality of your solution (or infeasibility)

MILP uses LP as a subroutine for solving relaxed problems. It also uses cuts and brach and bound. So there is a search tree.